The electrostatic potential inside a charged sphere is given as V=Ar2+B, where r is the disatance from the centre of the sphere, A and B are constant. Then, the charge density in the sphere is Solution in Telugu
16Aε0
6Aε0
20Aε0
−15Aε0
The correct Answer is:b
Let the volume charge density be ρ.
The electric field inside the charged sphere,
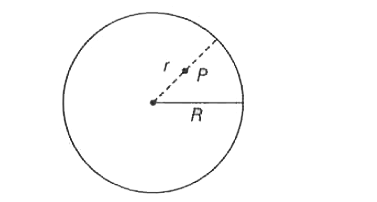
E=kqrR3
Where R = Radius of charged sphere
r = Distance of the point (P) inside the sphere
As volume charge density is ρ, then in terms of charge density
E=ρr3ε0
⇒ρ=3Eε0f
Now, electric field, E=−dVdr
Here, V=Ar2+B
∴E=−dVdr=−2Ar+0=−Ar
∴ρ=3Eε0r=−6Aε0)
Similar Questions
The potential of the field inside a charged sphere depends upon the distance from its centre to the point under consideration in the following way: V=ar^n+b , where a and b are constants If the charge is uniformly distributed within the sphere, then the value of n is
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View Solutionएक आवेशित गोलीय गेंद के भीतर स्थिरवैद्युत विभव ϕ=ar2+b द्वारा दिया गया है जहाँ r केन्द्र से दूरी है, a, b नियतांक है, तो गेंद के भीतर आवेश घनत्व है :
View SolutionThe electrostatic potential inside a charged spherical ball is given by phi=ar^2+b where r is the distance from the centre, a, b are constants.
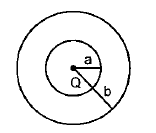
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively(see figure), has volume charge density ρ=Ar , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
View SolutionThe electrostatic potential inside a charged spherical ball is given by phi=ar^2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionThe electrostatic potential inside a charged spherical ball is given by phi=ar^2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
View Solution

