The equation of a travelling wave is
y(x,t)=0.02sin(x0.05+t0.01)m
Find (a) the wave velocity and
(b) the particle velocity at x=0.2mandt=0.3s.
The correct Answer is:A, B
To solve the problem, we will break it down into two parts: finding the wave velocity and finding the particle velocity.
Part (a): Finding the Wave Velocity
1. Identify the wave equation: The given wave equation is:
y(x,t)=0.02sin(x0.05+t0.01) m
2. Identify the wave parameters: From the wave equation, we can identify:
- The angular frequency ω is given by the coefficient of t:
ω=10.01=100 rad/s
- The wave number k is given by the coefficient of x:
k=10.05=20 rad/m
3. Calculate the wave velocity: The wave velocity v can be calculated using the formula:
v=ωk
Substituting the values of ω and k:
v=10020=5 m/s
Part (b): Finding the Particle Velocity
1. Find the partial derivative of y with respect to t: The particle velocity vp is given by:
vp=∂y∂t
We differentiate y(x,t):
∂y∂t=0.02⋅cos(x0.05+t0.01)⋅10.01
2. Substitute x=0.2m and t=0.3s: First, we calculate the argument of the cosine:
0.20.05+0.30.01=4+30=34
Therefore, we have:
∂y∂t=0.02⋅cos(34)⋅100
Simplifying this gives:
∂y∂t=2⋅cos(34)
3. Calculate the numerical value: Now we need to calculate 2⋅cos(34). Using a calculator:
cos(34∘)≈0.829
Thus:
vp≈2⋅0.829≈1.658 m/s
Final Answers
- (a) The wave velocity v is 5 m/s.
- (b) The particle velocity vp at x=0.2m and t=0.3s is approximately 1.658 m/s.
y(x,t)=0.02sin(x0.05+t0.01) m
- The angular frequency ω is given by the coefficient of t:
ω=10.01=100 rad/s
- The wave number k is given by the coefficient of x:
k=10.05=20 rad/m
v=ωk
Substituting the values of ω and k:
v=10020=5 m/s
vp=∂y∂t
We differentiate y(x,t):
∂y∂t=0.02⋅cos(x0.05+t0.01)⋅10.01
0.20.05+0.30.01=4+30=34
Therefore, we have:
∂y∂t=0.02⋅cos(34)⋅100
Simplifying this gives:
∂y∂t=2⋅cos(34)
cos(34∘)≈0.829
Thus:
vp≈2⋅0.829≈1.658 m/s
- (a) The wave velocity v is 5 m/s.
- (b) The particle velocity vp at x=0.2m and t=0.3s is approximately 1.658 m/s.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 Single Correct
5 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 More Than One Correct
6 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 1 Objective
6 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionA transverse wave travelling on a stretched string is is represented by the equation
y=2(2x−6.2t)2+20. Then ,
View SolutionThe equation of a wave is given by Y=5sin10π(t−0.01x) along the x-axis. (All the quantities are expressed in SI units). The phase difference between the points separated by a distance of 10m along x-axis is
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
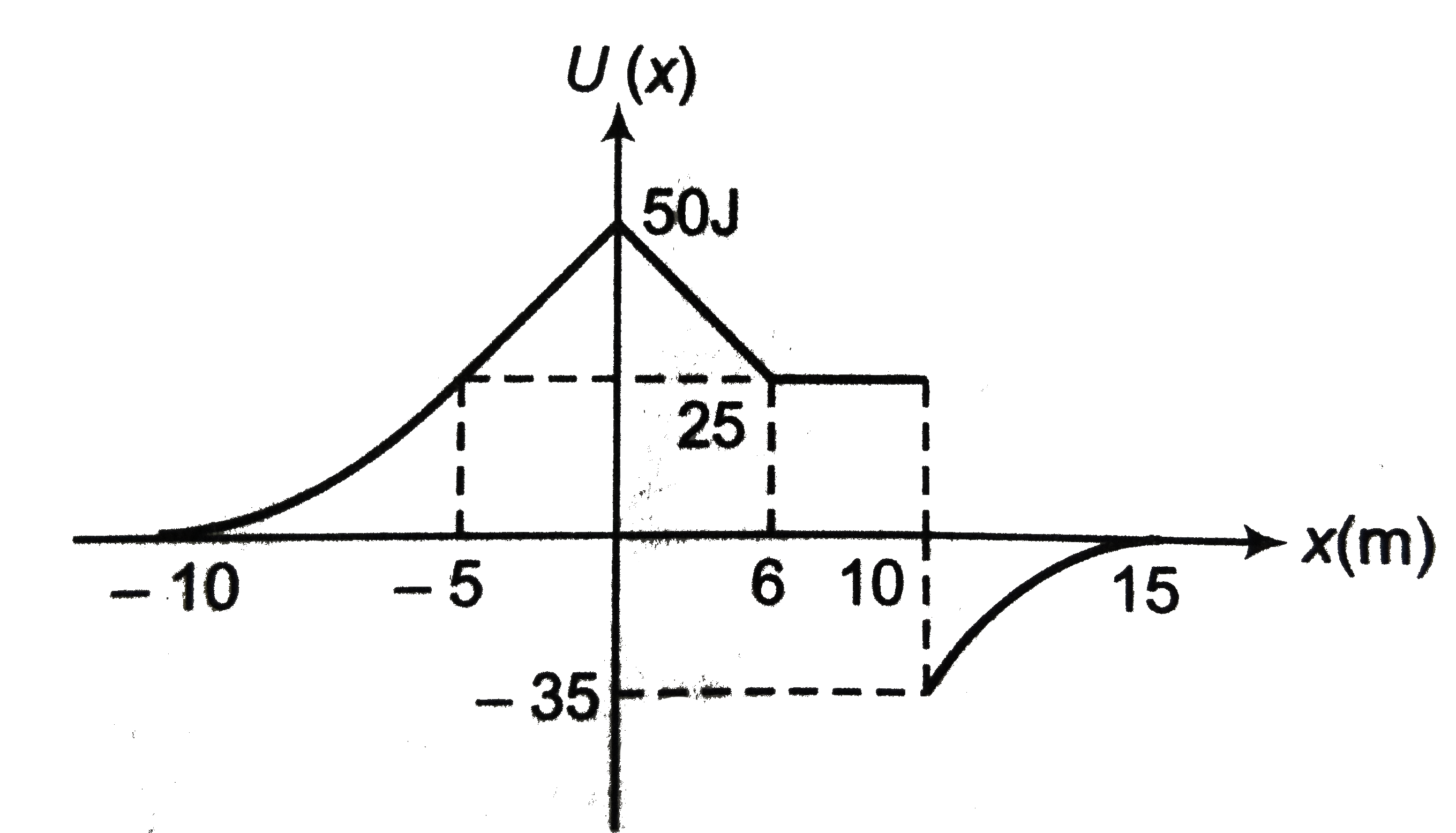
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionThe equation of a wave is
y=(x,t)=0.05sin[π2(10x−40t)−π4]m
find: (a) the wavelength, the frequency and the wave velocity
(b) the participle velocity and acceleration at x=0.5mand t=0.05s.
View SolutionThe equation of a travelling wave is y(x, t) = 0.02 sin ((x)/(0.05) + (t)/(0.01)) m Find (a) the wave velocity and (b) the particle velocity at x = 0.2 m and t = 0.3 s . Given cos theta = -0.85 , where theta = 34 rad
View SolutionA wave represented by the given equation Y = A sin (10 pi x + 15 pi t + (pi)/(3)) , where x is in meter and t is in second. The expression represents (1) A wave travelling in the negative X direction with a velocity of 1.5 m/sec (2) A wave travelling in the negative X direction with a wavelength of 0.2 m (3) A wave travelling in the positive X direction with a velocity of 1.5 m/sec. (4) A wave travelling in the positive X direction with a wavelength of 0.2 m
View SolutionA wave is represented by the equation y=0.5sin(10t−x)m. It is a travelling wave propagating along the + x direction with velocity
View SolutionThe equation of progressive wave is y=a sin (200 t-x) . where x is in meter and t is in second. The velocity of wave is
View SolutionThe equation of progressive wave is y = 0.2 sin 2pi [(t)/(0.01)-(x)/(0.3)] , where x and y are in metre and t is in second. The velocity of propagation of the wave is
View Solutionकिसी अनुप्रस्थ तरंग का समीकरण y=Asin2π(tT−xλ) है। कण का अधिकतम वेग, तरंग वेग का चार गुना है जबकि :
View SolutionA progressive wave is represented by an equation y=5sin(80πt−0.5πx), where x, y are in 'm' and 't' in 's'. Find (a) amplitude (b)wavelength (c ) frequency (d) velocity of the wave.
View SolutionThe equation of a wave is,
y(x,t)=0.05sin[π2(10x−40t)−π4]m Find,
The wavelength, the frequency and the wave velocity.
(ii) The particle velocity and acceleration at x=0.5 m and t=0.05 s.
View SolutionThe equations of a transverse wave is given by y=0.05sinπ(2t−0.02x), where x,y are in metre and t is in second. The minimum distance of separation between two particles which are in phase and the wave velocity are respectively…….
View Solution

