The half cycle of an alternating singnal is shown in fig. It increases uniformly form zero at 0∘→Fmat(α)∘ and decrease uniformly from (Fm)at180∘

The average value of the singnal is
(π+α)Fmπ
(π−α)Fmπ
(π+α3π)Fm
(2π+α2π)Fm
The correct Answer is:B
For finding the average value m, we would find the total area of the trapezium and divide it by (π).
Area=2×ΔOAE+rectang≤ABDE
=2×(1/2)×Fm0α+(π−2α)Fm0=(π−α)Fm
Average value =(π−α)Fm/(π)
rms value: From similar triangles , we get
ytˆa=Fmα or (y2)=F2mα2tˆa2
This gives the equation of the single over the two triangles OAE and DBC. The single reamins constant over the angle α to (π−α), i.e., over an angluar distance of (π−α)−α=(π−2α).
Sum of the square
2f2mα2F2m(π−4α3)
The mean value of the squares
=1πF2m(π−4α3)=F2m(1−4α3π)
rms value =Fm√(1−4α3π).
Topper's Solved these Questions
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Integer
Explore 4 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Archives Subjective
Explore 1 Video
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Assertion-reasoning
Explore 7 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
Similar Questions
The half cycle of an alternating singnal is shown in fig. It increases uniformly form zero at 0∘→Fmat(α)∘ and decrease uniformly from (Fm)at180∘

The effective value of the singnal is
View SolutionIf the current in the toroidal solenoid increases uniformly from zero to 6.0 A in 3.0μs Self-inductance of the toroidal solenoid is 40μ H The magnitude of self-induced emf is
View SolutionThe time required for a 50 Hz sinusoidal alternating current to changed its value from zero to the r.m.s. value
View SolutionA particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .
.
View SolutionA particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .
.
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimensional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is
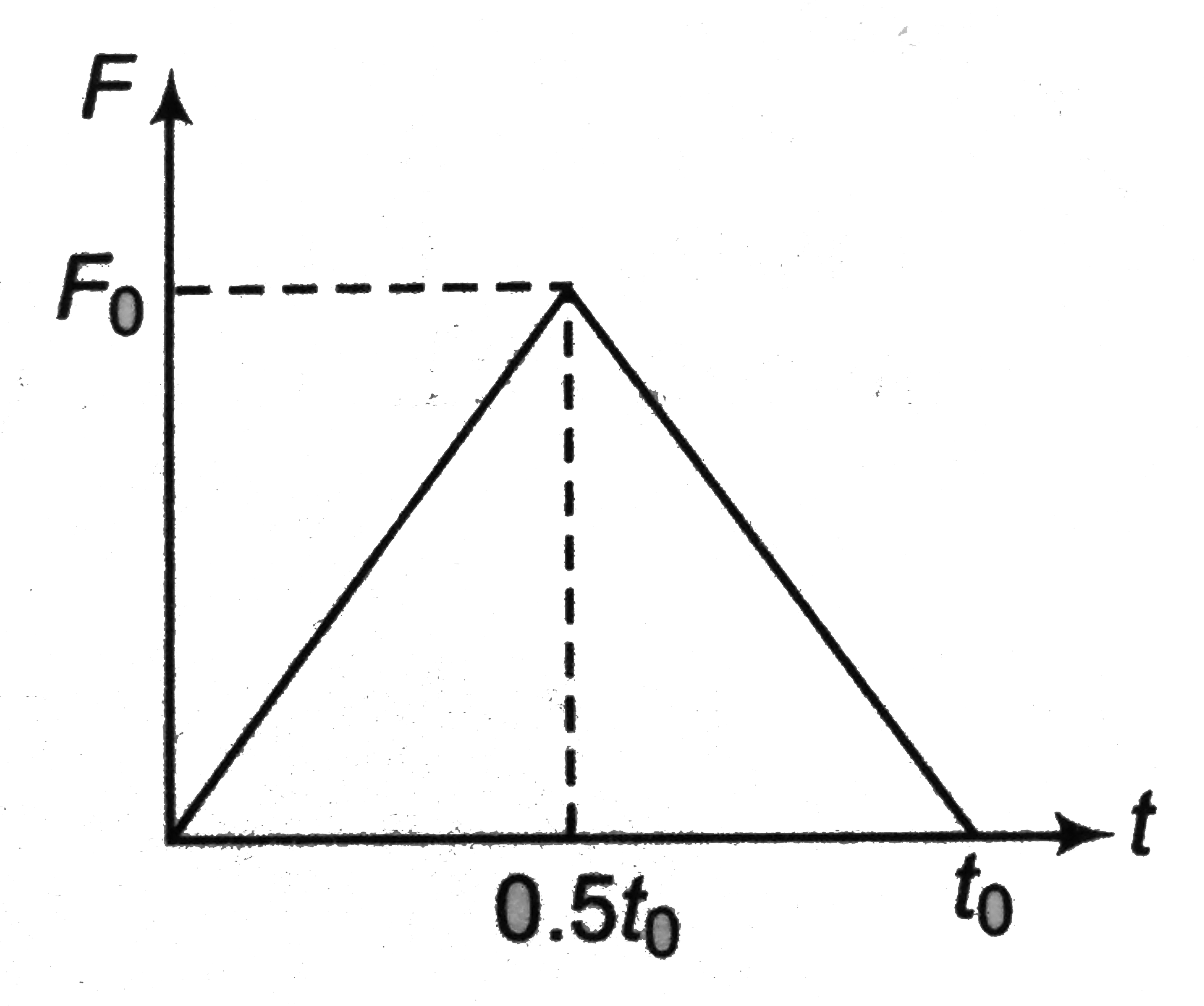
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is

View SolutionA block of mass 10 kg accelerates uniformly from rest to a speed of 2 m/s in 20 sec. The average power developed in time interval of 0 to 20 sec is
View SolutionA particle starting from rest has a constant acceleration of 4m/s2 for 4 s. It then retards uniformly for next 8 s and comes to rest. Find during the motion of particle (a) average acceleration (b) average speed and (c) average velocity.
View SolutionA car starts moving along a line, first with acceleration a=5m/s2 starting from rest then uniformly and finally decelerating at the same rate till it comes to rest. The total time of motion is 25s. The average speed during the time is 20m/s. The particle moves uniformly for (2.5x) second. Find the value of x.
View Solution
