The linear density of a vibrating string is 10−4kg/m. A transverse wave is propagating on the string, which is described by the equation y=0.02sin(x+30t), where x and y are in metres and time t in seconds. Then tension in the string is
The correct Answer is:0.117
Step by step video solution for The linear density of a vibrating string is 10^(-4) kg//m. A transverse wave is propagating on the string, which is described by the equation y=0.02 sin (x+30t), where x and y are in metres and time t in seconds. Then tension in the string is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Subjective Type
Explore 2 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension Type
Explore 5 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Multiple Correct Answers Type
Explore 5 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
A standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
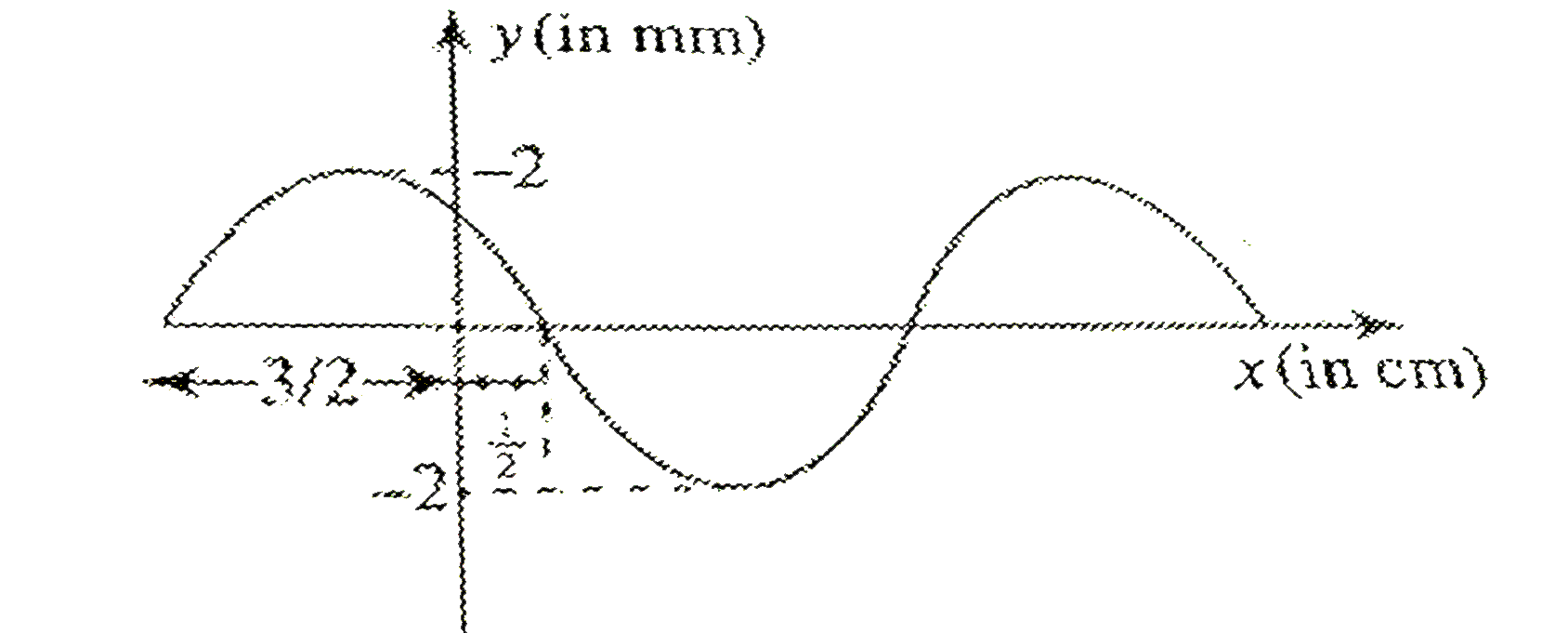
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionTwo wave function in a medium along x direction are given by
y1=12+(2x−3t)2m, y2=−12+(2x+3t−6)2m
Where x is in meters and t is in seconds
View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionDuring the adiabatic expansion of 2 moles of a gas, the internal energy of the gas is found to decrease by 2 joules , the work done during the process on the gas will be equal to
View SolutionThe equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string is
View SolutionThe linear density of a vibrating string is 10−4kg/m. A transverse wave is propagating on the string, which is described by the equation y=0.02sin(x+30t), where x and y are in metres and time t in seconds. Then tension in the string is
View SolutionA transverse periodic wave on a string with a linear mass density of 0.200 kg/m is described by the following equation y=0.05 sin (420t-21.0 x) where x and y are in metres and t is in seconds.The tension in the string is equal to :
View SolutionThe linear density of a vibrating string is 1.3 xx 10^(-4) kg//m A transverse wave is propagating on the string and is described by the equation y= 0.021 sin (x + 30 t) where x and y are measured in meter and t t in second the tension in the string is :-
View SolutionA string is producing transverse vibration whose equation is y = 0.021 sin ( x + 30 t ) , where x and y are in metre and t is in second . If the linear density of the string is 1.3×10−4kg/m , then tension in string in newton will be
View SolutionThe linear density of a vibrating string is 2xx10^(-4) kg/m. A transverse wave is propagating on the string and is described by the equation y=0.021 sin (x + 30 t) where x and y are in metre and t is in second. The tension in the string is
View SolutionA transverse wave described by y=0.5sin(x+40t) is propagating on a vibrating string of linear density 0.01 kg/m. If x and y are in metre and time is in second, then the tension in the wire is
View SolutionThe equation of a transverse wave propagating in a string is y=0.02sin(x-30t) . Hwere x and y are in metre and t is in second. If linear density of the string is 1.3xx10^(-4)kg//m , then the tension in the string is :
View SolutionA transverse wave propagating on a stretched string of linear density 3×10−4kg−m−1 is represented by the equation
y=0.2sin(1.5x+60t)
Where x is in metre and t is in second. The tension in the string (in Newton) is
View SolutionA transverse wve given by Y = 0.021 sin (x + 30t) is propagating in a string of linear density 1.3 x, 10^(-4) kg/m. If x and y are in metres and time in seconds , the tension in string is :
View SolutionA transverse wave propagating on the string can be described by the equation y=2sin(10x+300t) where x and y are in metres and t in second.If the vibrating string has linear density of 0.6×10−3gcm ,then the tension in the string is
View Solution
