The magnetic field at the centre of a circular coil of radius r is π time that due to a long straight wire at a distance r from it for equal currents. The following figure show three cases. In all cases the circular part has radius r and straight ones are infinitely long. For same current, the B field at the centre P in cases 1, 2, 3, has the ratio

(−π2):(π2):(3π4−12)
(−π2+1):(π2+1):(3π4+12)
−π2:π2:3π4
(−π2−1):(π1−14):(3π4+12)
The correct Answer is:A
Similar Questions
Knowledge Check
Figure shows three cases: in all case the circular part has radius r and straight ones are infinitely long. For the same current the ratio of field B at centre P in the three case B1:B2:B3 is
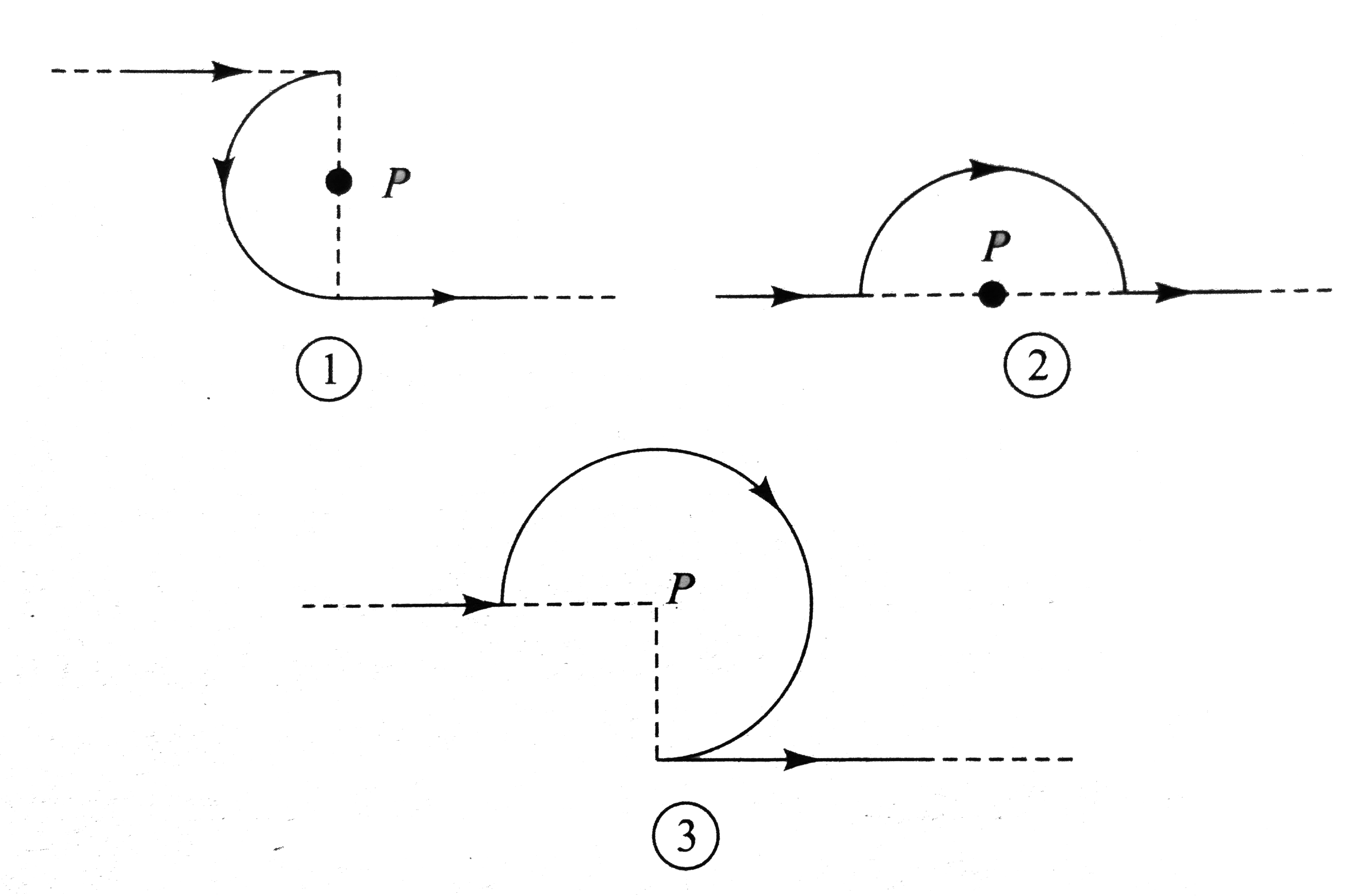 A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C(−π2):(π2):(3π4)D(−π2−1):(π2−14):(3π4+12)
A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C(−π2):(π2):(3π4)D(−π2−1):(π2−14):(3π4+12)The magnetic field at the centre of a circular current carrying coil of radius r is Be. The magnetic on its axis at a distance r from the centre is Ba. The value of Be:Ba will be :
A1 : √2B1 : 2√2C2√2 : 1D√2 : 1What will be magnetic field at centre of current carrying circular loop of radius R?
Aμ0I4πRBμ0I2πRCμ0I2RDzero
What will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionThe magnetic field at the centre of a circular coil of radius r carrying current l is B1. The field at the centre of another coil of radius 2r carrying same current l is B2. The ratio B1B2 is
View SolutionThe magnetic field at the centre of a circular coil of radius r carrying current l is B1. The field at the centre of another coil of radius 2r carrying same current l is B2. The ratio B1B2 is
View Solution