The orbital angular momentum of electron in the n1th shell of element of atomic number Z1isL1 an the same in the n2th shell of element of atomic number Z2isL2 If L2>L1 then
n2>n1
Z2>Z1
n2Z2>n1Z1
Both (a) and (b)
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the orbital angular momentum of electrons in different shells of atoms with different atomic numbers.
1. Understanding Orbital Angular Momentum:
The orbital angular momentum L of an electron in a shell is given by the formula:
L=nh2π
where n is the principal quantum number (shell number) and h is Planck's constant.
2. Expressing Angular Momentum for Different Shells:
For the n1 shell of an element with atomic number Z1:
L1=n1h2π
For the n2 shell of an element with atomic number Z2:
L2=n2h2π
3. Given Condition:
We are given that L2>L1. This implies:
n2h2π>n1h2π
Since h2π is a constant, we can simplify this to:
n2>n1
4. Analyzing Atomic Numbers:
The problem does not provide a direct relationship between the atomic numbers Z1 and Z2 and the angular momentum. Therefore, we cannot conclude that Z2>Z1 based solely on the angular momentum comparison.
5. Conclusion:
From the above analysis, we can conclude that if L2>L1, then it must be true that:
n2>n1
However, we cannot make any conclusions about the relationship between Z1 and Z2.
Answer:
The correct option is that n2>n1.
The orbital angular momentum L of an electron in a shell is given by the formula:
L=nh2π
where n is the principal quantum number (shell number) and h is Planck's constant.
For the n1 shell of an element with atomic number Z1:
L1=n1h2π
For the n2 shell of an element with atomic number Z2:
L2=n2h2π
We are given that L2>L1. This implies:
n2h2π>n1h2π
Since h2π is a constant, we can simplify this to:
n2>n1
The problem does not provide a direct relationship between the atomic numbers Z1 and Z2 and the angular momentum. Therefore, we cannot conclude that Z2>Z1 based solely on the angular momentum comparison.
From the above analysis, we can conclude that if L2>L1, then it must be true that:
n2>n1
However, we cannot make any conclusions about the relationship between Z1 and Z2.
The correct option is that n2>n1.
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - ASSERTION AND REASON
10 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MATCH THE COLUMNS
4 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
Similar Questions
Assertion: Angular momentum of single electron in any orbit or hydrogen type atom is independent of the atomic number of the element.
Reason: In ground state angular momentum is minimum
View SolutionIn Column I physical quantities corresponding to hydrogen and hydrogen like atom are given. In column II, powers of principal quantum number n are givem on which thosee physical quantities depend. Match the two columns.
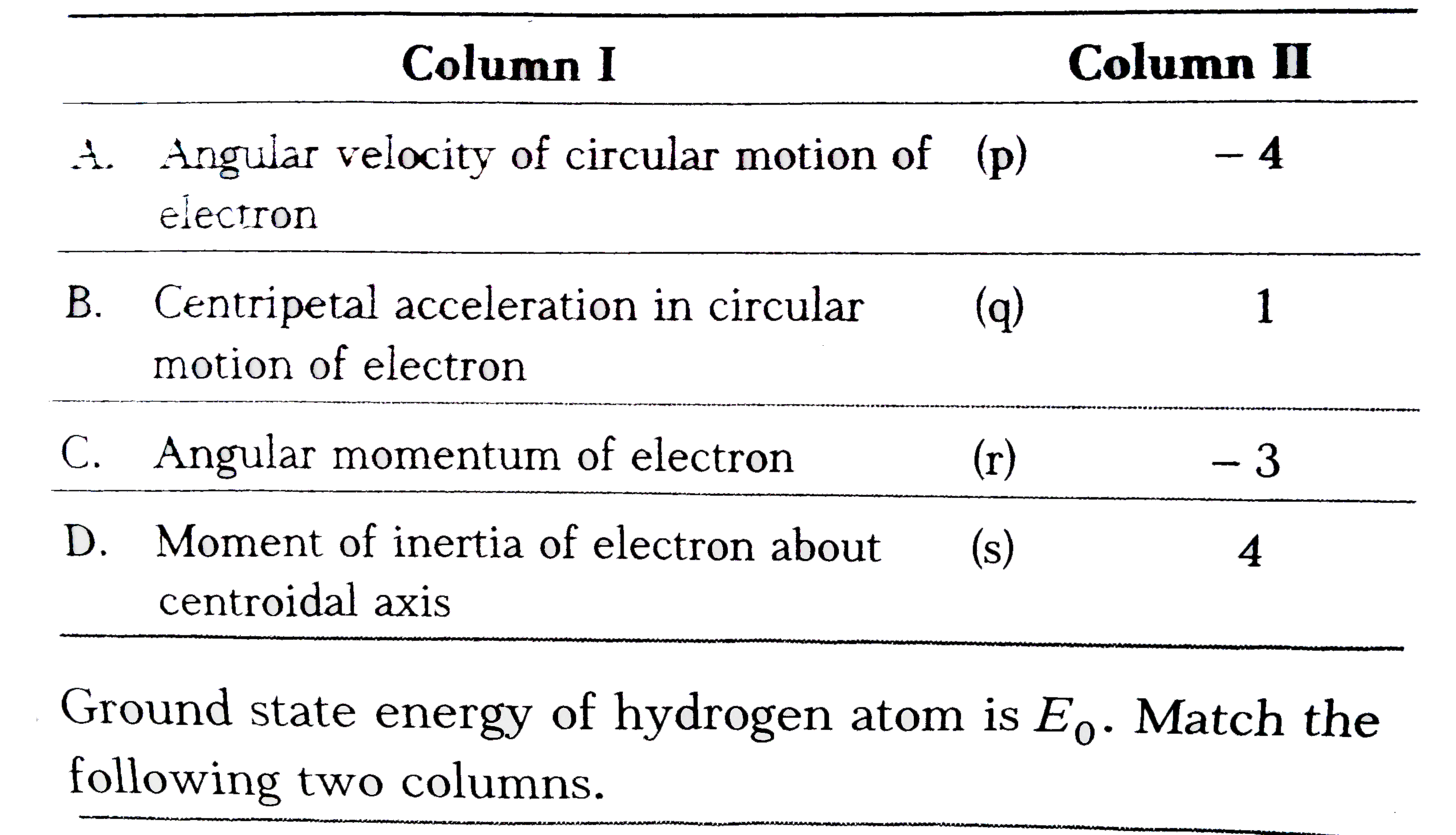
View SolutionX-rays were discovered by
View SolutionIn the given arrangement, the loop is moved with consisant velocity in uniform magnetic field B in a restricted a region of width a. The time for which the emf is induced in the cirucit is

View SolutionIn the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is
View SolutionShow that if the axes are rectangular,the equation of the line through the point (x_(1),y_(1),z_(1)) at right angle to the lines (x)/(l_(1))=(y)/(m_(1))=(z)/(n_(1));(x)/(l_(2))=(y)/(m_(2))=(z)/(n_(2)) is (x-x_(1))/(m_(1)n_(2)-m_(2)n_(1))=(y-y_(1))/(n_(1)l_(2)-n_(2)l_(1))=(z-z_(1))/(l_(1)m_(2)-l_(2)m_(1))
View SolutionThe orbital angular momentum of electron in the n1th shell of element of atomic number Z1isL1 an the same in the n2th shell of element of atomic number Z2isL2 If L2>L1 then
View Solution
If the direction cosines of two lines are (l1,m1,n1) and
(l2,m2,n2) and the angle between them is θ then
l21+m21+n21=1=l22+m22+n22
and costheta=l1l2+m1m2+n1n2
If the angle between the lines is 60∘ then the value
of l1(l1+l2)+m1(m1+m2)+n1(n1+n2) is
View SolutionShow that the matris ⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ is orthogonal,
ifl21+m21+n21=Σl21=1=Σl22=Σ23and
l1l2+m1m2+n1n2=Σl1l2=0=Σl2l3=Σl3l1.
View Solutionu=v=w=1 के लिए, यदि n1n2l1l2=(a+bb+c), तब
View SolutionIf (l1,m1,n1),(l2,m2,n2) are D.C's of two lines, then (l1m2−l2m1)2+(m1n2−n1m2)2+(n1l2−n2l1)2+(l1l2+m1m2+n1n2)2=
View Solutionयदि (l1,m1,n1),(l2,m2,n2) और (l3,m3,n3) तीन परस्पर लब सरल रेखाओ की दिककोज्याए हो , तो सिद्ध कीजिए की l1m2n2−m3n2=m1n2l3−n3l2=n1l2m3−l3m2=±1]
View SolutionThe straight lines x−x1l1=y−y1m1=z−z1n1 and xl2=ym2=zn2 will be perpendicular, if -
View SolutionIf (l1,m1,n1),(l2,m2,n2) are d.c's of two lines then find the value of (l1m2−l2m1)2+(m1n2−n1m2)2+(n1l2−n2l1)2+(l1l2+m1m2+n1n2)2
View SolutionShow that the condition that tha concurrent lines with direction cosines (l1.m1,n1),(l2,m2,n2)and(l3,m3,n3) are coplanar is l1(m2n3−m3n2)+m1(n2l3−n3l2)+n1(l2m3−l3n2)=0
View Solution

