The potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
(a) Zero
(b) √2Em
(c) √Em
(d) √3E2m
The correct Answer is:A
From the conservation of energy
KE+PE=E or KE=E−12kx2
KE at x=−√2Ek is E−12k(2Ek)=0
The speed of particle at x=−√2Ek is zero.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Referring the graphs, which of the following is/are correc?

View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
When the cord is burnt with a match releasing the spring, the two masses fly apart with equal
View SolutionIn figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
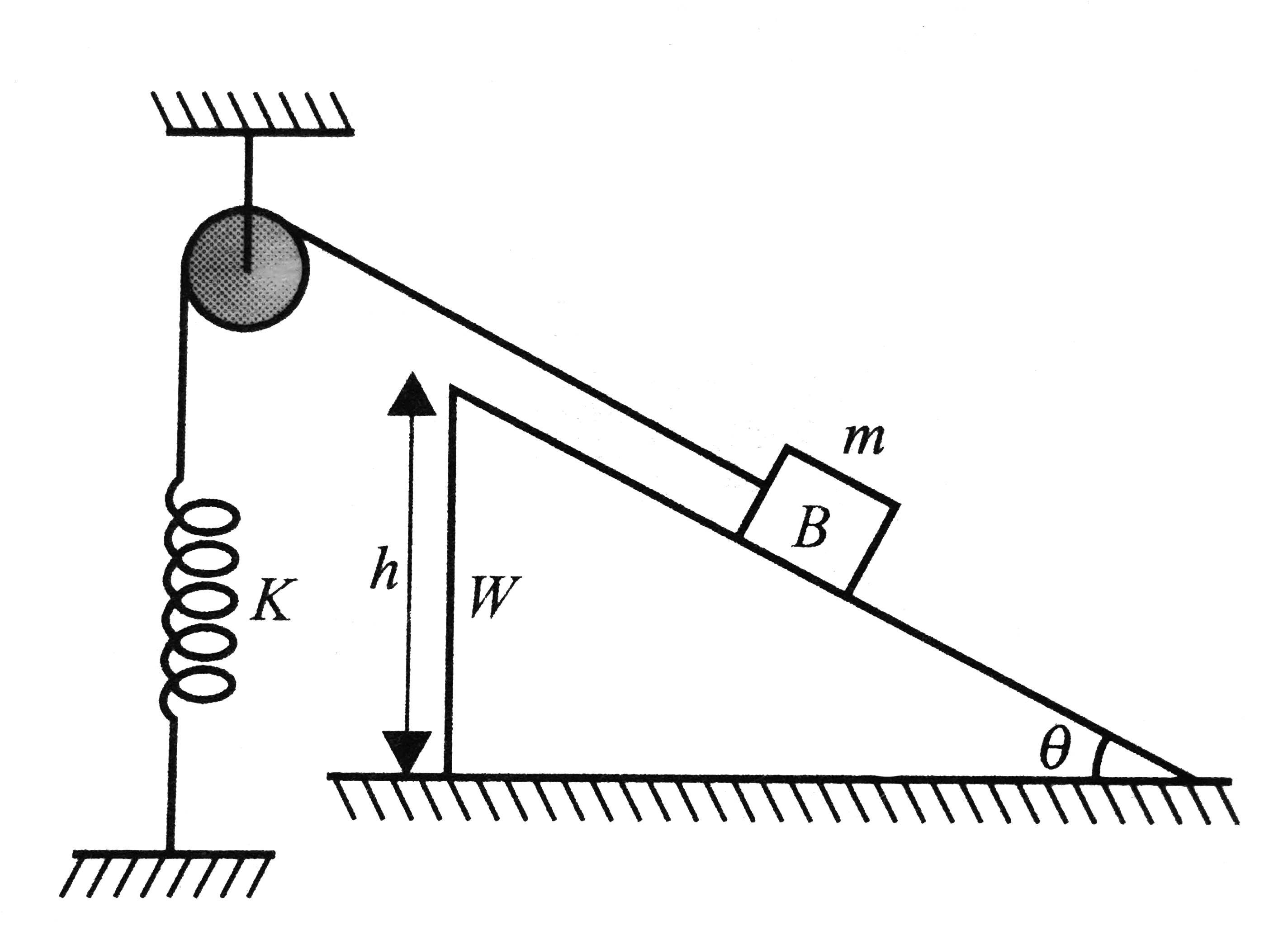
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1//2)kx^2 for xlt0 and U=0 for xge0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=-sqrt(2E//k) is
View SolutionThe potential energy of a particle of mass m is given by U = (1)/(2) kx^(2) for x lt 0 and U=0 for x ge 0 . If total mechanical energy of the particle is E . Then its speed at x = sqrt((2E)/(k)) is
View SolutionThe total mechanical enegry of a particle is E. The speed of the particle at x=(2EK)1/2 is (2Em)1/2. Find the potential energy of the particle at x :
View SolutionThe potential energy of a particle of mass m is given by U=(1)/(2)kx^(2) for x lt 0 and U = 0 for x ge 0 . If total mechanical energy of the particle is E. Then its speed at x = sqrt((2E)/(k)) is
View SolutionThe potential energy of a particle of mass m is given by U(x){E00≤x<10x>1
λ1 and λ2 are the de-Broglie wavelength of the particle, when 0≤x≤1 and x>1 respectively. If the total energy of particle is 2E0, then the ratio λ1λ2 will be
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0andU=0 for x≥0. If total mechanical energy of the particle is E, is speed at x=√2Ek is
View SolutionThe potential energy of a particle of mass m is given by U(x)=E00≤x≤10 x>1 λ1 and λ2 are the de-Broglie wavelengths of the particle, when 0≤x≤1 and x > 1 respectively. If the total energy of particle is 2E0. find (λ1/λ2)2
View SolutionA particle is constrained to move in the region x ge 0 and its potential energy is given by U=2x^(4)-3x^(2)J (where x is in m) For what values of x, the particle is under Stable equilibrium
View SolutionA particle is constrained to move in the region x ge 0 and its potential energy is given by U=2x^(4)-3x^(2)J (where x is in m) For what values of x, the particle is under Unstable equilibrium
View SolutionX - अक्ष पर स्वतन्त्र रूप से दोलन कर रहे 1 किग्रा द्रव्यमान के कण की स्थितिज ऊर्जा U=x42−x22 जूल है | यदि कण की सम्पूर्ण यांत्रिक ऊर्जा 6 जूल है तो उसकी अधिकतम चाल होगी :
View SolutionX - अक्ष पर स्वतंत्र रूप से दोलन कर रहे 1किग्रा द्रव्यमान के कण की स्थितिज ऊर्जा U=x44−x22 जूल है। यदि कण की सम्पूर्ण यांत्रिक जूल 2 है तो उसकी अधिकतम चाल होगी -
View Solution

