The ratio of pressure of the same gas in two containers is n1T1n2T2 where n1 & n2 are the number of moles and T1 & T2 are respective temperatures. If the containers are now joined find the ratio of final pressure to the temperature :
P1T2+P2T12T1T2
P1T1+P2T1T1T2
P1T1+P2T22T1T2
none of these
The correct Answer is:A
To solve the problem, we need to find the ratio of the final pressure to the temperature after the two containers of gas are joined. We will use the ideal gas law and the relationship between pressure, volume, temperature, and the number of moles.
1. Understanding the Initial Conditions:
- We have two containers with gases at different pressures, temperatures, and number of moles.
- The ratio of the pressures of the gases in the two containers is given by:
P1P2=n1T1n2T2
2. Using the Ideal Gas Law:
- The ideal gas law states that:
PV=nRT
- For both containers, we can express the pressures as:
P1=n1RT1VandP2=n2RT2V
3. Combining the Containers:
- When the two containers are joined, the total volume becomes 2V.
- The total number of moles of gas after mixing is n1+n2.
4. Applying the Ideal Gas Law to the Combined System:
- The pressure P in the combined volume can be expressed as:
P⋅(2V)=(n1+n2)RT
- Rearranging gives:
P=(n1+n2)RT2V
5. Finding the Ratio of Final Pressure to Temperature:
- We need to find the ratio PT:
PT=(n1+n2)R2V
6. Substituting for P1 and P2:
- From the earlier expressions for P1 and P2:
P1=n1RT1VandP2=n2RT2V
- We can express n1 and n2 in terms of P1 and P2:
n1=P1VRT1andn2=P2VRT2
7. Substituting Back into the Ratio:
- Substitute n1 and n2 into the ratio:
PT=(P1VRT1+P2VRT2)R2V
- Simplifying gives:
PT=12(P1T1+P2T2)
8. Final Result:
- Thus, the final ratio of pressure to temperature after the containers are joined is:
PT=12(P1T1+P2T2)
- We have two containers with gases at different pressures, temperatures, and number of moles.
- The ratio of the pressures of the gases in the two containers is given by:
P1P2=n1T1n2T2
- The ideal gas law states that:
PV=nRT
- For both containers, we can express the pressures as:
P1=n1RT1VandP2=n2RT2V
- When the two containers are joined, the total volume becomes 2V.
- The total number of moles of gas after mixing is n1+n2.
- The pressure P in the combined volume can be expressed as:
P⋅(2V)=(n1+n2)RT
- Rearranging gives:
P=(n1+n2)RT2V
- We need to find the ratio PT:
PT=(n1+n2)R2V
- From the earlier expressions for P1 and P2:
P1=n1RT1VandP2=n2RT2V
- We can express n1 and n2 in terms of P1 and P2:
n1=P1VRT1andn2=P2VRT2
- Substitute n1 and n2 into the ratio:
PT=(P1VRT1+P2VRT2)R2V
- Simplifying gives:
PT=12(P1T1+P2T2)
- Thus, the final ratio of pressure to temperature after the containers are joined is:
PT=12(P1T1+P2T2)
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Multiple Corrects
Explore 28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Assertion-Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Subjective
Explore 22 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
Similar Questions
For an ideal gas
View SolutionStatement I: A quasi -static process is so called bacause it is a sudden and large change of the system.
Statement II: An adiabatic process is not quasi- static because it is a sudden and large change of the system.
View SolutionFive grams of helium having rms speed of molecules 1000m/s and 24g of oxygen having rms speed of 1000m/s are introduced into a thermally isolated vessel. Find the rms speeds of helium and oxygen individually when thermal equilibrium is attained. Neglect the heat capacity of vessel.
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
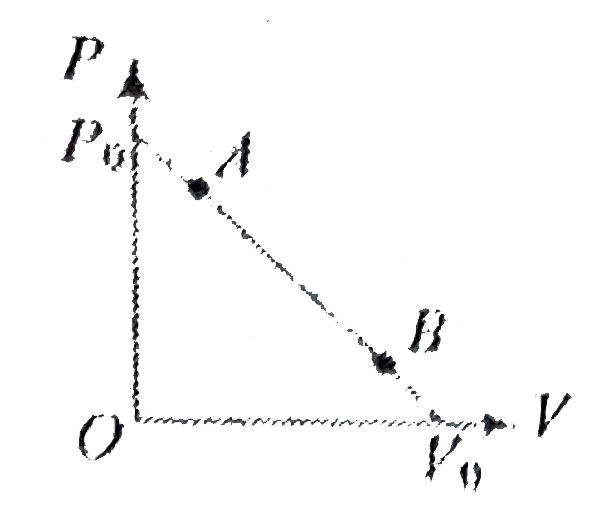
The absolute temperature T versus volume V for the given process is
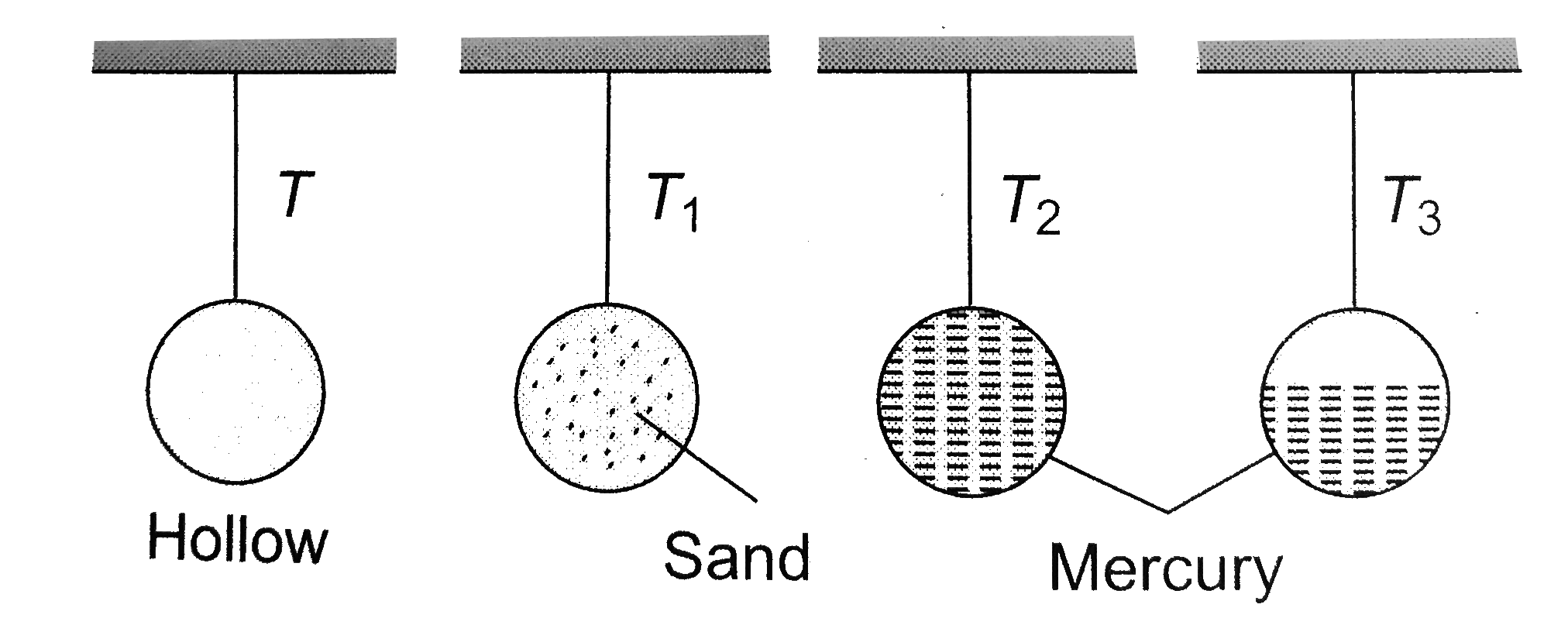
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
View SolutionTwo perfect monoatomic gases at absolute temperature T_(1) and T_(2) are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases are n_(1) and n_(2) .
View SolutionThe ratio of pressure of the same gas in two containers in (n_(1) T_(1))/(n_(2) T_(2)) where n_(1) & n_(2) are the number of moles and T_(1) & T_(2) are respective temperatures. If the containers are now joined find the ratio of pressure to the pressure :
View SolutionThree perfect gases at absolute temperature T_(1), T_(2) and T_(3) are mixed. The masses f molecules are m_(1), m_(2) and m_(3) and the number of molecules are n_(1), n_(2) and n_(3) respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionTwo perifect gases at absolute temperatures T1andT2 are mixed. The absolute temperature of the mixture is T. there is no loss of energy.If m1andm2 are masses of molecules and n1andn2 are number of molecules, then
View SolutionIf Nt=Noeλt then number of disintefrated atoms between t1 to t2(t2>t1) will ve :-
View Solutionतीन आदर्श गेसों को जिनके परम ताप T1,T2 तथा T3 है मिश्रित किया जाता है। इनके अणुओं के द्रव्यमान क्रमश: m1,m2 तथा m3 है और अणुओं की संख्या क्रमशः n1,n2 तथा n3 है। यदि ऊर्जा का क्षय नहीं हो मिश्रण का अन्तिम ताप है:
View SolutionTwo perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View SolutionUnder similar conditions of temperature and pressures, if the time taken for effusion of the same volume of H_(2),N_(2) and CO_(2) gas through the same porour wall are t_(1),t_(2) and t_(3) respectively, then arrange t_(1),t_(2) and t_(3) in their increasing order.
View SolutionThree perfect gases at absolute temperatures T1,T2andT3 are mixed. The masses of molecules are m1,m2andm3 and the number of molecules are n1,n2andn3 respectively. Assuming no less of energy, the final temperature of the mixture is:
View SolutionTwo perfect gases at absolute temperatures T_(1) and T_(2) are mixed.There is no loss of energy .Find the temperature of the mixture if the masses of the molecules are m_(1) and m_(2) and the number of molecules in the gases are n_(1) and n_(2)
View Solution
