
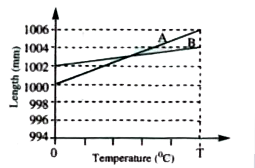
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
αA=3×10−6/∘C,500∘C
αA=3×10−6/∘C,222.22∘C
αA=27×10−6/∘C,500∘C
αA=27×10−6/∘C,222.22∘C
The correct Answer is:D
Slope of line A=(1006−1000)mmT∘C=ΔLΔT=LαA
i.e., 6Tmm/∘C=(1000mm)αA
similary for line B
2Tmm/∘C=(1002mm)αB
Dividing Eq. (i) by Eq. (ii)
3=1000αA1002αB≈=3α=3αB
From Eq. (iii) αA=3×9×10−6=27×10−6/∘C
from eq. (i) T=61000αA=6×1061000×27
=222.22∘C
Similar Questions
The coefficient of linear expansion for a certain metal varies with temperatures as α(T). If L0 is the initial length of the metal and the temperature of the metal is changed from T0 to (T0>T), then
View SolutionThe variation of length of two metal rods A and B with change in temperature are shown in fig. The coefficients of linear expansion αA for the metal A and the temperature T will be (Given αa=9×10−6/°C )
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion alpha . Find increase in length when temperature changes from T to T+ DeltaT
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionThe corfficient of linear expansion for a certain metal varies with temperature as α(T). If L0 is the initial elgnth of the metal and the temperature of metal is changed from T0 to T(T0>T), then
View SolutionThe variation of lengths of two metal rods A and B with change in temperature are as shown in the figure. The ratio of αBαA is (Here αA= Linear coefficient of thermal expansion of rod A3αB= Linear coefficient of thermal expansion of rodB .
'(##CEN_KSR_PHY_JEE_C13_E01_016_Q04##)'
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
View Solution
