The variation of PE of harmonic oscillator is as shown in the figure. The spring constant is

A
1×102Nm−1
B
1.5×102Nm−1
C
2×102Nm−1
D
3×102Nm−1
Text Solution
The correct Answer is:B
12kA2=(0.04−0.01)J=0.03J
∴ k=0.06A2=0.06(0.02)2=15×102Nm−1
|
Topper's Solved these Questions
- OSCILLATIONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:OSCILLATIONSExercise:MHT CET CORNER
Explore 29 Videos
- OSCILLATIONSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:OSCILLATIONSExercise:EXERCISE 1
Explore 67 Videos
- MOCK TEST 5Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MOCK TEST 5Exercise:MCQs
Explore 42 Videos
- PRACTICE SET 01Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 01Exercise:PAPER 1 (PHYSICS & CHEMISTRY)
Explore 50 Videos
Similar Questions
Knowledge Check
The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
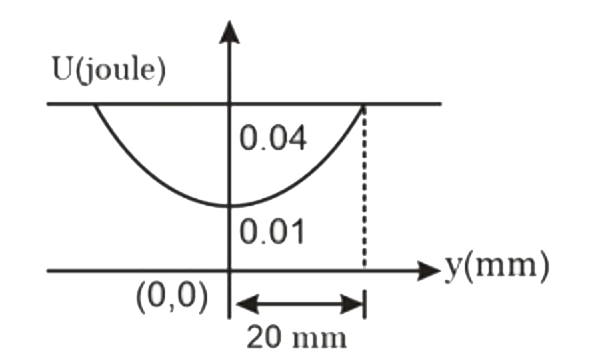 A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1
A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1The veriation of potential energy of harmonic escillator is as shown in figure. The spring constant is
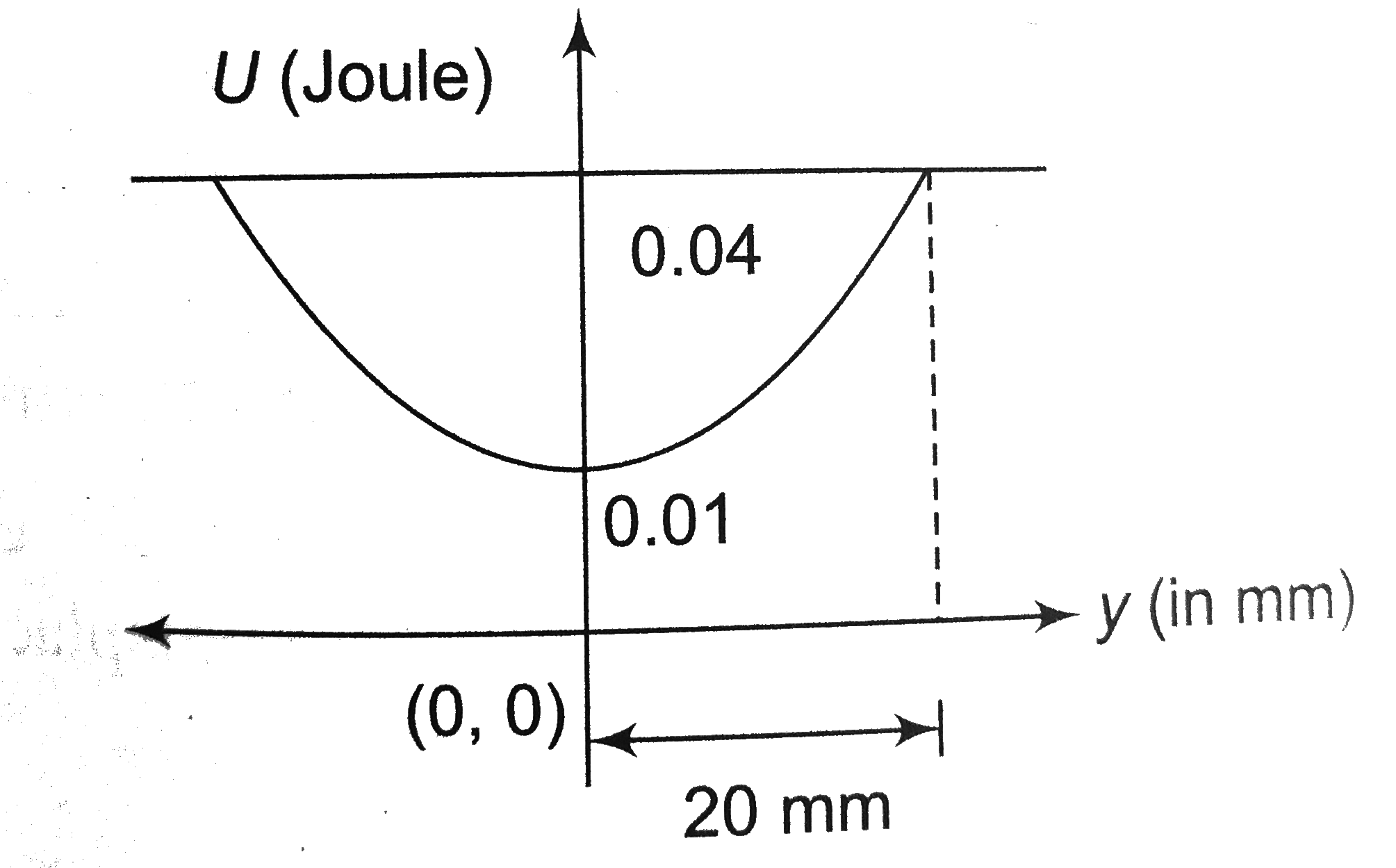 A1×102N/mB150N/mC0.667×102N/mD3×102N/m
A1×102N/mB150N/mC0.667×102N/mD3×102N/mThe variation of potenial energy of harmoic oscillartor is as show in figure . The spring constant is
 A1×102N/mB150N/mC0.667×102N/mD3×102N/m
A1×102N/mB150N/mC0.667×102N/mD3×102N/m
The variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

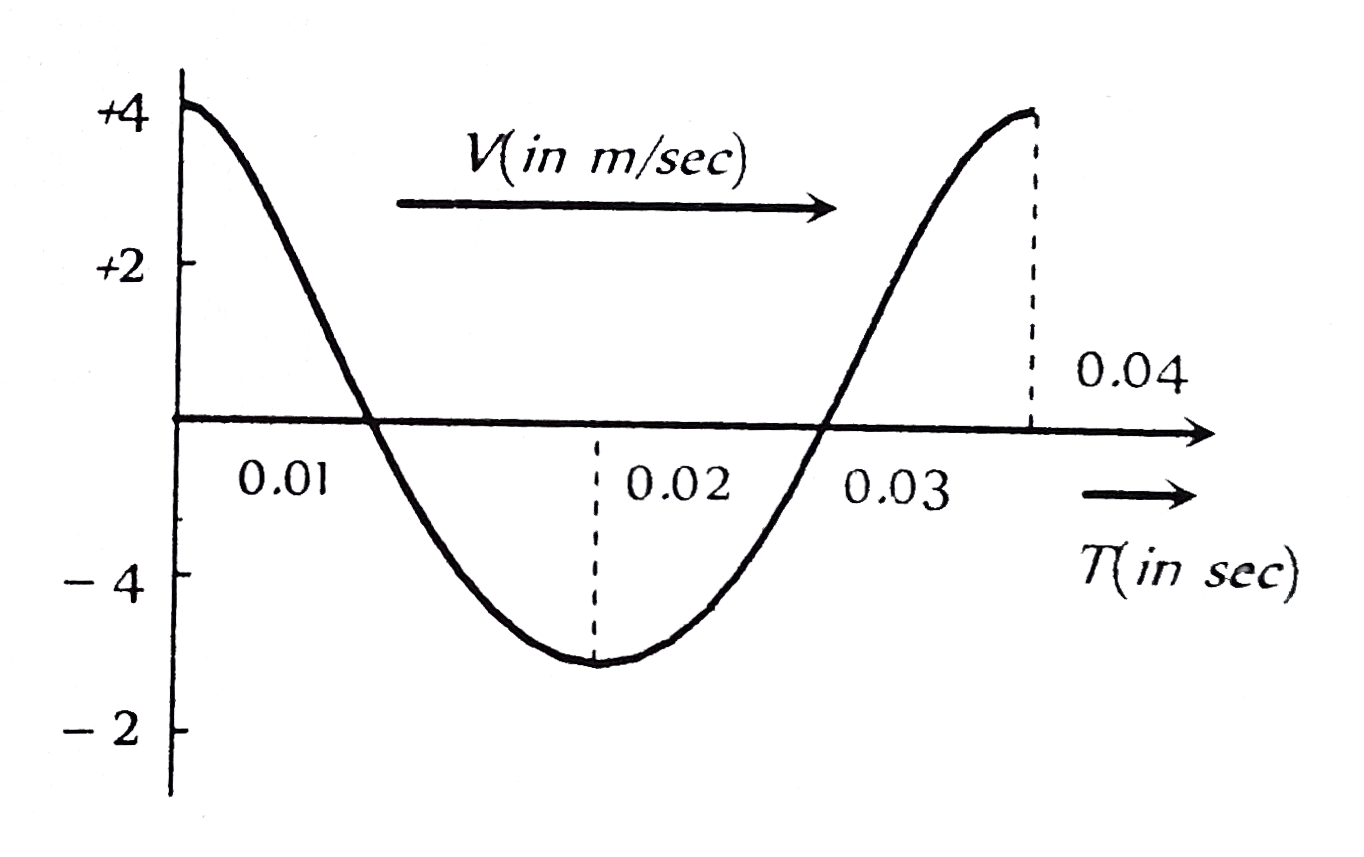
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
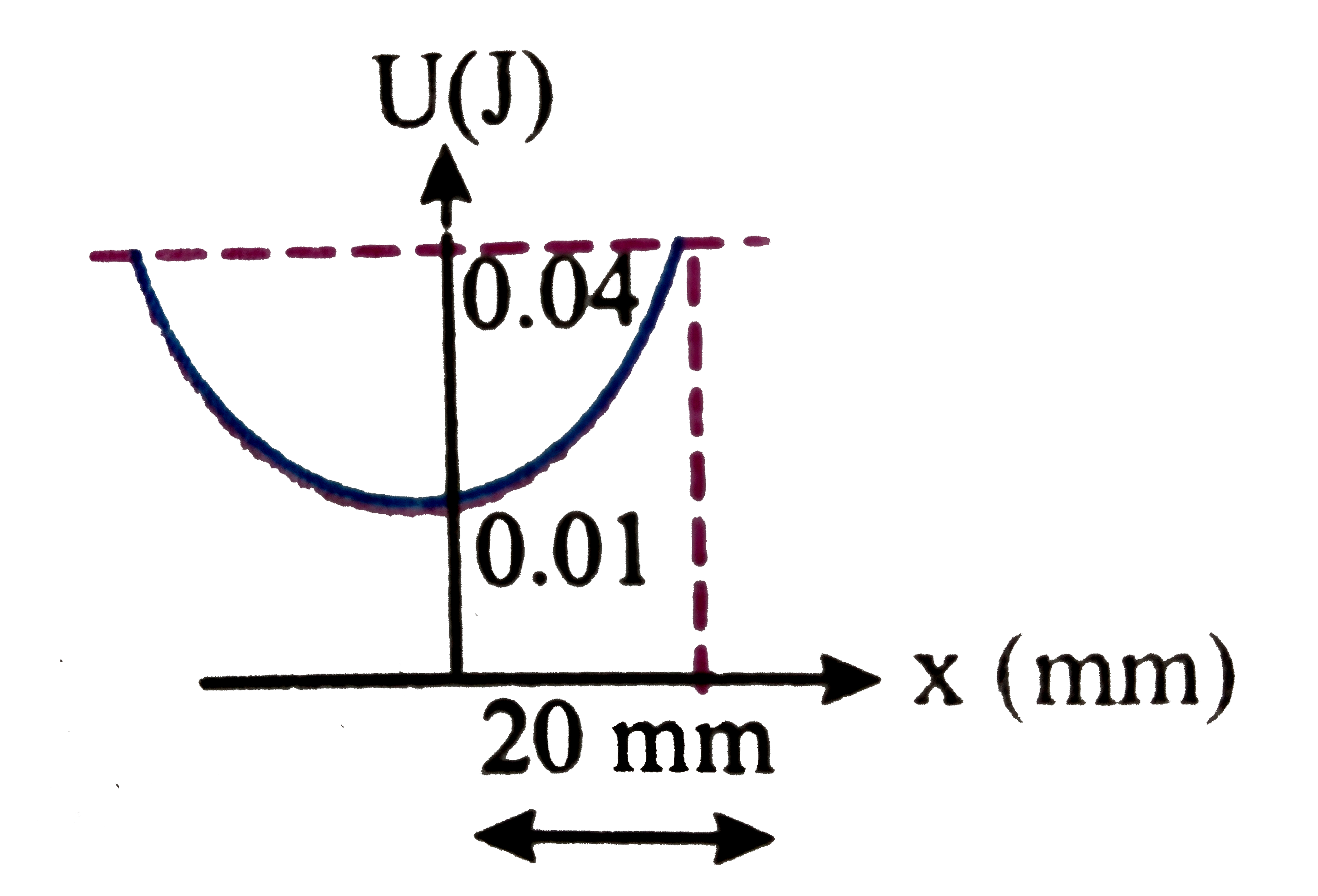
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
View SolutionThe frequency of oscillation of the spring shown in the figure will be
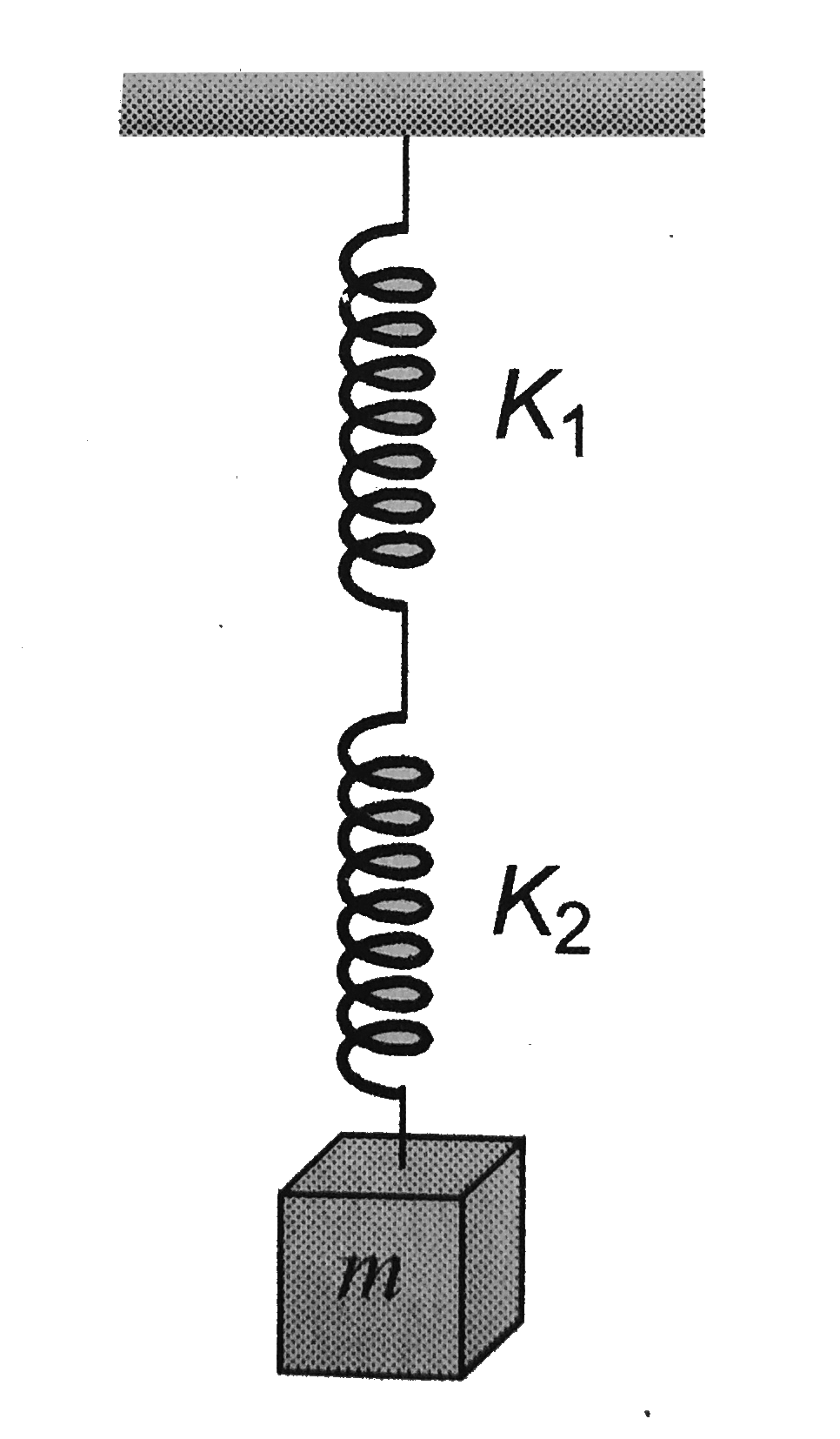
View SolutionThe frequency of oscillation of the springs shown in the figure will be

View Solution

