Three identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12 V battery as shown in Fig
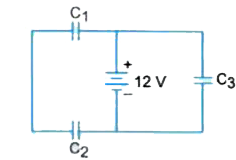
charge on each capacitor
The capacitor arrangement can be redrawn as shown in Fig
Combined capacitance of series arrangement of C1 and C2 is C12=C1×C2C1+C2=6×66+6μF=3μF
∴q1=q2=C12.V=3μF×12V=36μC and q3=C3V=6μF×12V=72μC
Similar Questions
Three identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12V battery as shown in Fig. Find
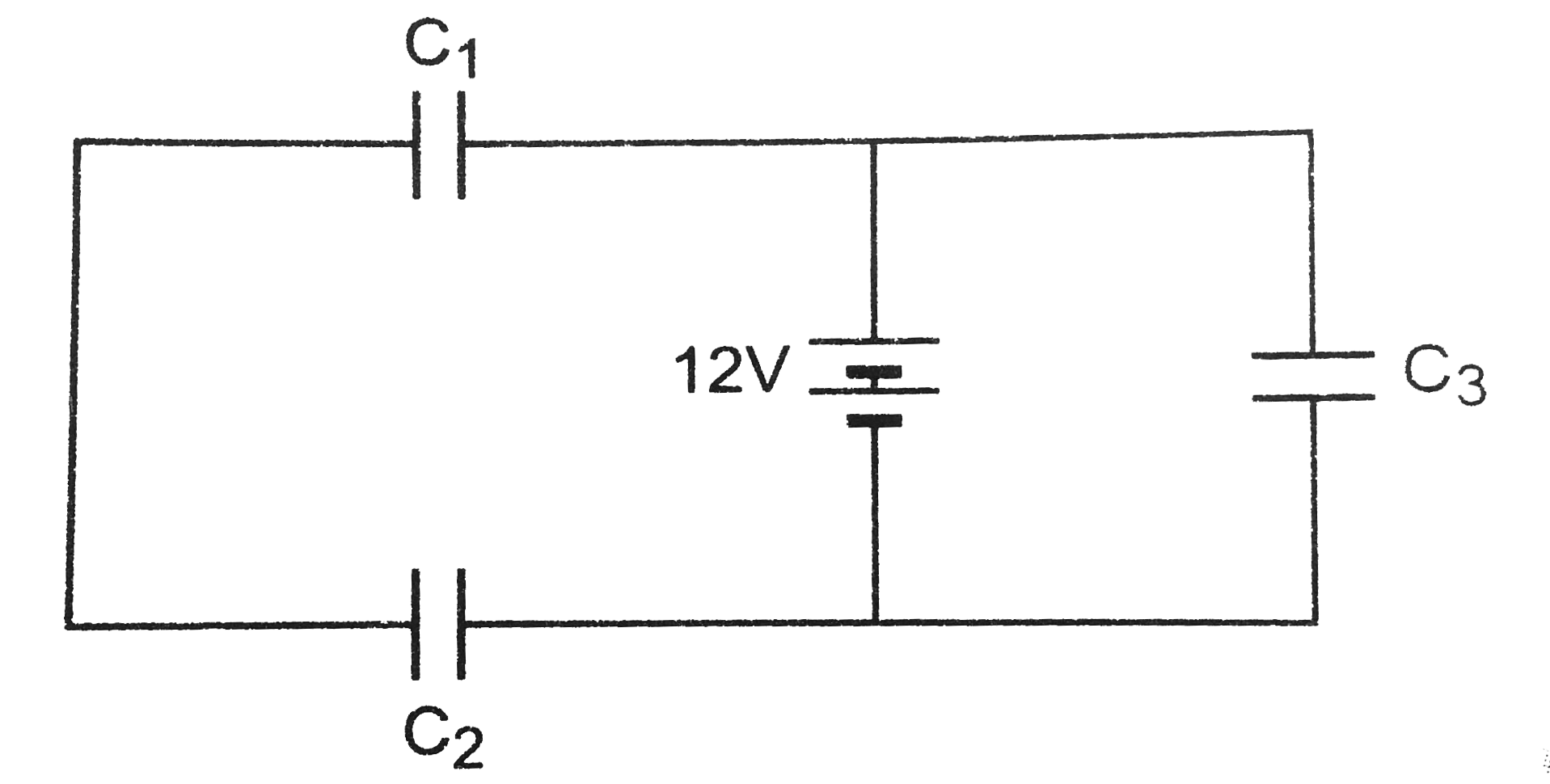
(i) charge on each capacitor
(ii) equivalent capacitance of the network.
(iii) energy stored in the network of capacitors.
View SolutionThree identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12V battery as shown in Fig. Find
(i) charge on each capcitor
(ii) equivalent capacitance of the network.
(iii) energy stored in the network of capacitors.

View SolutionThree identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12 V battery as shown in Fig
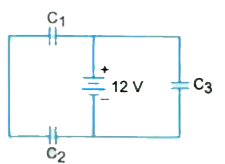
equivalent capacitance of the network
View SolutionThree identical capacitors C1,C2 and C3 of capacitance 6μF each are connected to a 12 V battery as shown in Fig
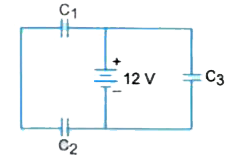
energy stored in the network of capacitors .
View SolutionTwo capacitors C1 and C2 are connected to a battery of 6V as shown in Fig. Find the charge on each capacitor.
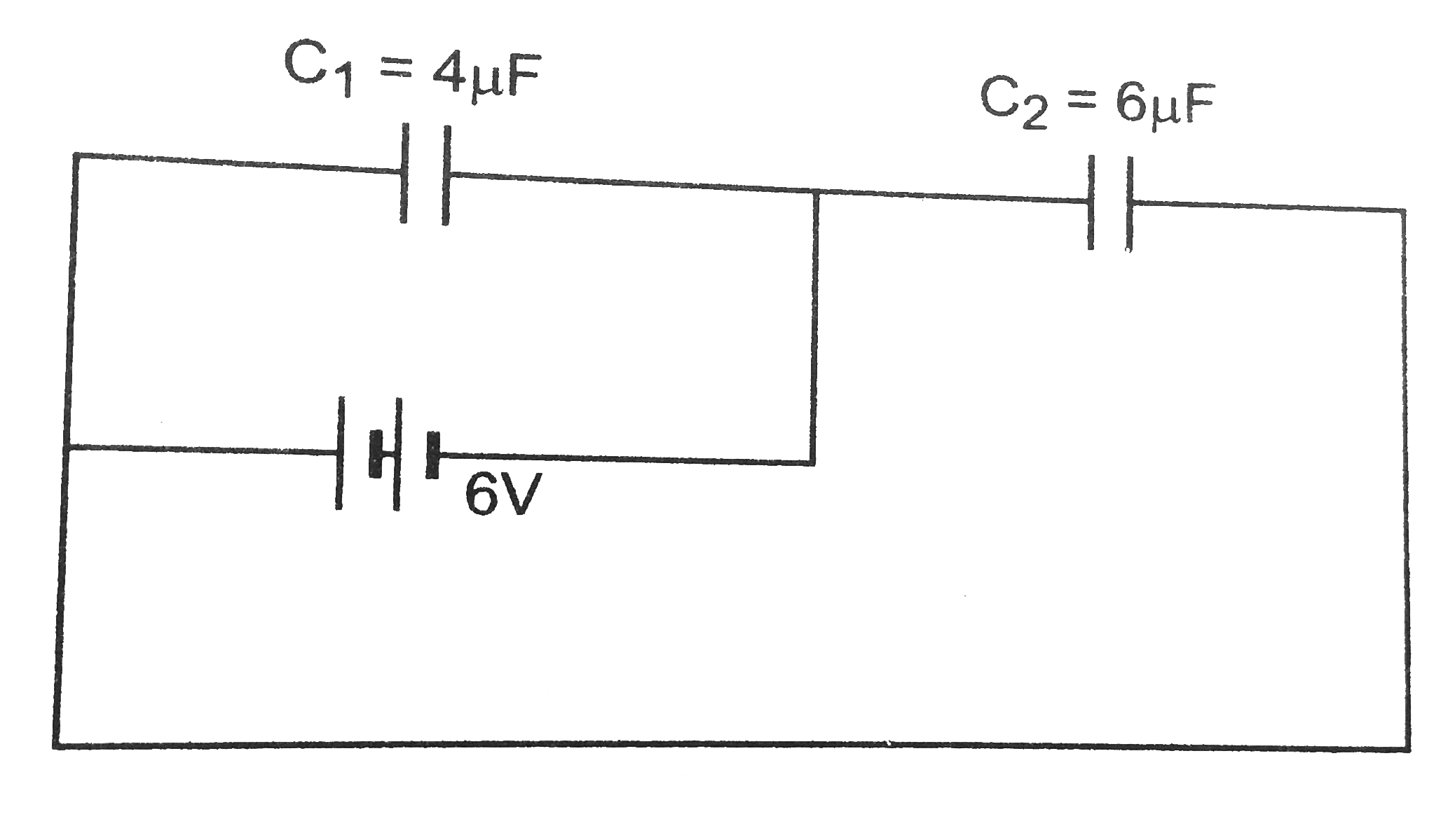
View SolutionThree capacitors C1=6μF,C2=12μF and C3=20μF are connected to a 100 V battery, as shown in figure below:
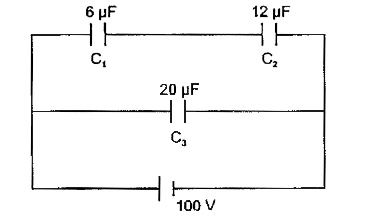
(i) Charge on each plate of capacitor C1.
(ii) Electrostatic potential energy stored in capacitor C3.
View SolutionThree capacitors C1,C2andC3 are connected to a 6 V battery, as shown in Fig. Find the charges on the three capcitors.

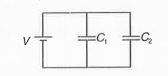
View SolutionTwo capacitors C1 and C2 of capacitances C2 and C4 are connected to a V volt battery, as shown in figure. The ratio of energy slored in capacitors C1 and C2 is
View SolutionThree capacitors C1=3μF,C2=6μFandC3=10μF are connected to a 50 V battery as shown in the figure below:
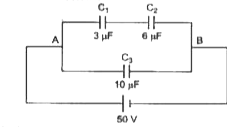
Calculate :
The charge on C1
View SolutionThree capacitors C1=3μF,C2=6μFandC3=10μF are connected to a 50 V battery as shown in the figure below:
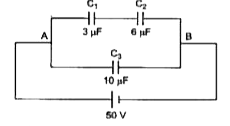
Calculate :
The equivalent capacitance of the circuit between points A and B.
View Solution

