Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
t=dv
t=3d2v
t=2d3v
t=0
The correct Answer is:C
Velocity of A is v along AB. Velocity of B is along BC. Its
component along BA is vcos60∘=v/2. Thus, the separation AB
decreases at the rate
v+v2=3v2
Since, this rate is consonant, the time taken in reducing the
separation AB from d to zero is
t=d3v/2=2d3v
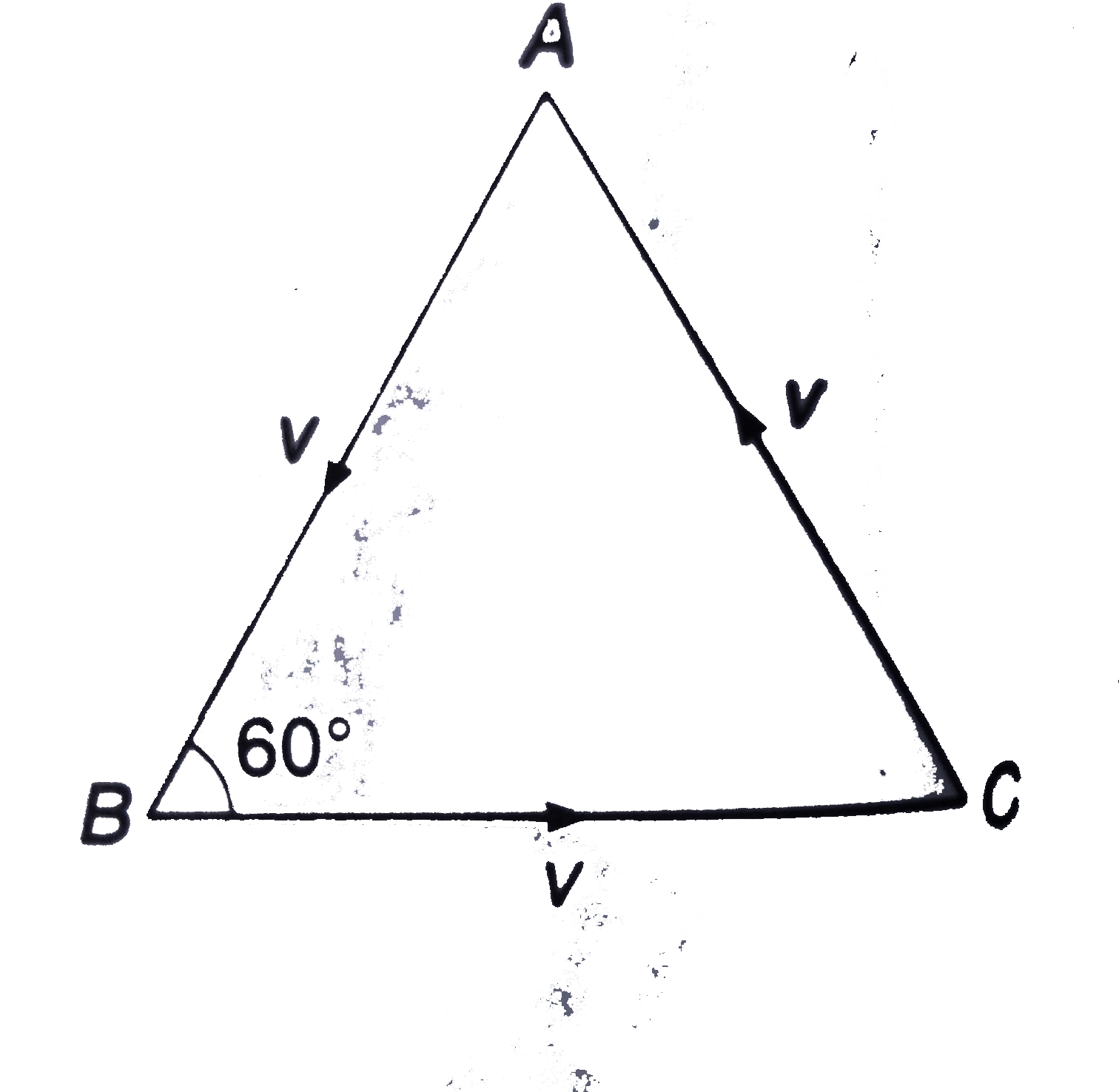
Similar Questions
Four particles A,B,CandD are situated at the cornerst of a square ABCD of side aatt−0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CB~andD along DA. At what time will these particles meet each other ?
View SolutionThree boys A,B and C are situated at the vertices of an equilateral triangle of side d at t=0. Each of the boys moves with constant speed v. A always moves towards C and C towards A, At what time and where they meet each other?
View Solution
Knowledge Check
Three particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
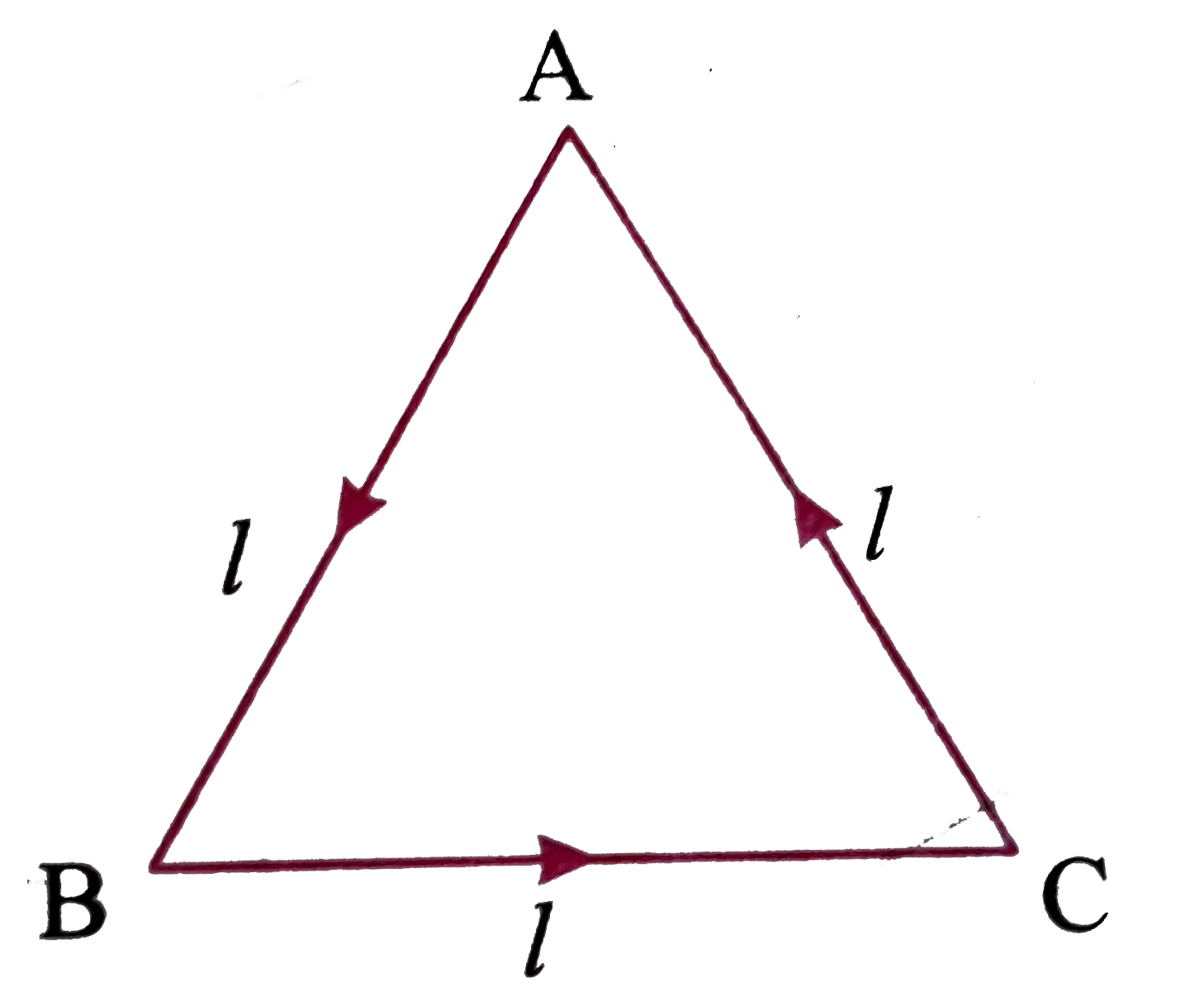 AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2
AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2Three particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
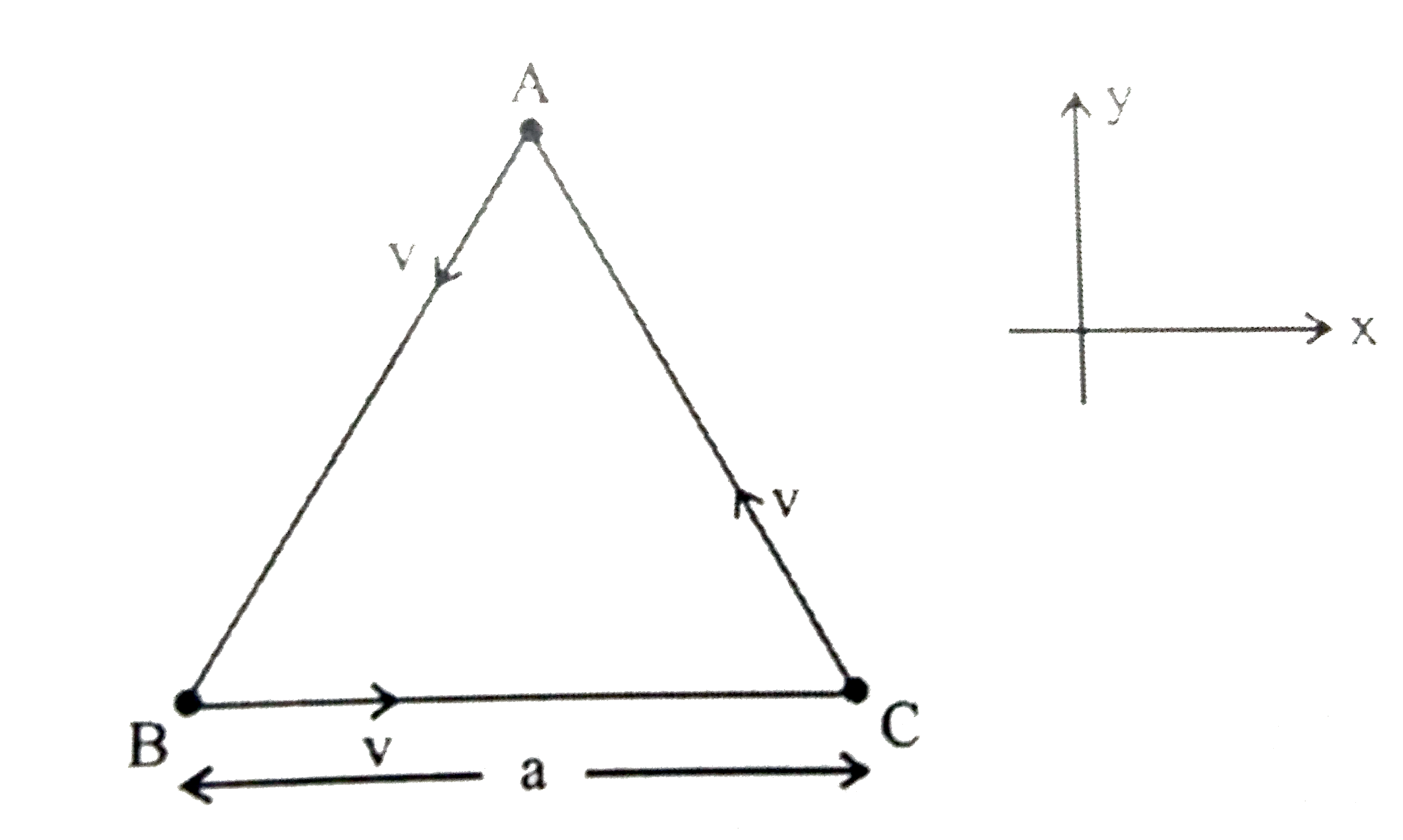 AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-direction
AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-directionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2b
Three particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
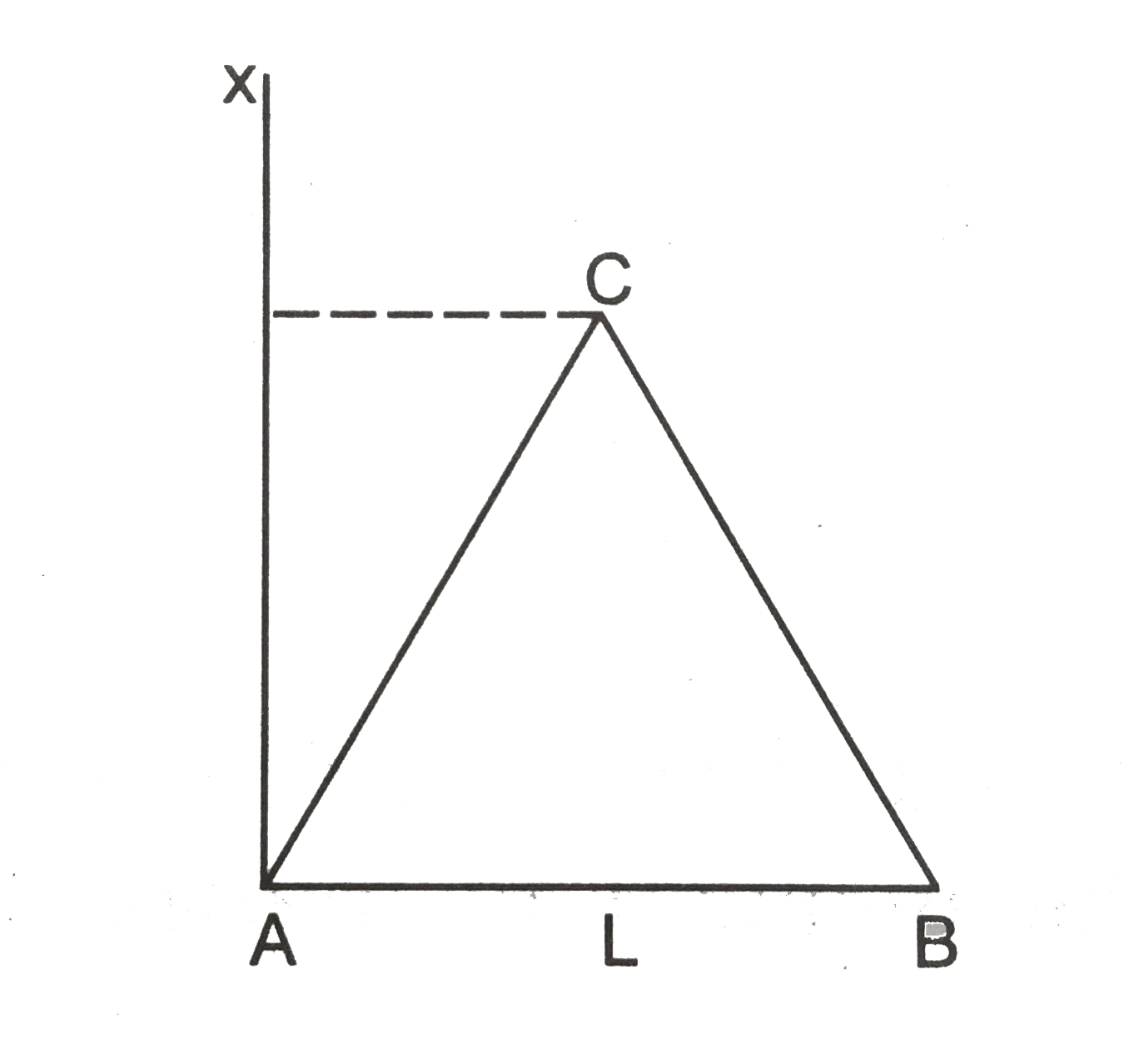
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
View SolutionThree insects A,B and C are situated at the vertices of an equillateral triangle of side 1. the insect A heads towards B,B towards C,C towards A with constant speeds v such that they always remain at the vertices of an equilateral triangle. Find the (a) time of their meeting (b) equation of path traced by one insect relative to the other.
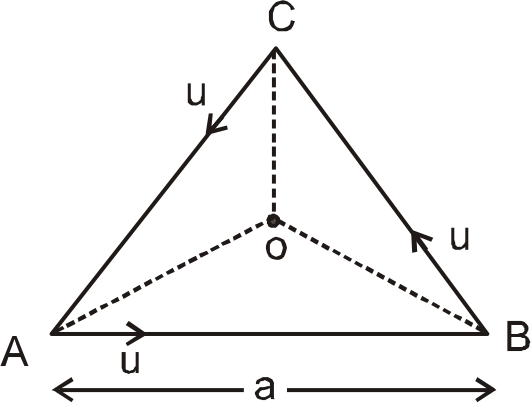
View SolutionThree particles A,B and C situated at vertices of an equilateral triangle, all moving with same constant speed such that A always move towards B,B always towards C and C always towards A. Initial seperation between each of the particle is a. O is the centroid of the triangle. Distance covered by particle A when it completes one revolution around O is
View SolutionThree identical particles are located at the vertices of an equilateral triangle. Each particle moves along a meridian with equal speed towards the centroid and collides inelastically.
View Solution

