Total energy of a particle executing oscillating motionis 3 joule and given by
E=x2+2x+v2−2v
Where x is the displacement from origin at x=0 and v is velocity of particle at x. Then choose the correct statements)
Amplitude of osciallation is 1m
Maximum velocity of particles during oscillation is 3m/sec.
Amplitude of oscillation is 2m
Maximum velocity of particle during oscillation is (√5+1) m/sec.
The correct Answer is:C, D
To solve the problem, we need to analyze the given expression for the total energy of a particle executing oscillatory motion:
E=x2+2x+v2−2v
We know that the total energy E is given as 3 Joules.
Step 1: Set Up the Equation
We start by substituting the total energy into the equation:
3=x2+2x+v2−2v
Step 2: Analyze at Extreme Position
At the extreme position of oscillation, the velocity v is zero. Thus, we can simplify the equation:
3=x2+2x+02−2(0)
3=x2+2x
Step 3: Rearranging the Equation
Rearranging gives us:
x2+2x−3=0
Step 4: Factor the Quadratic Equation
Next, we can factor this quadratic equation:
(x+3)(x−1)=0
Step 5: Solve for Displacement
Setting each factor to zero gives us the possible values for x:
1. x+3=0 → x=−3
2. x−1=0 → x=1
Since x represents displacement, the maximum displacement (amplitude) is:
A=1meter
Step 6: Maximum Velocity Calculation
To find the maximum velocity, we analyze the total energy at the mean position (where x=0). Substituting x=0 into the energy equation:
3=02+2(0)+v2−2v
3=v2−2v
Step 7: Rearranging for Velocity
Rearranging gives us:
v2−2v−3=0
Step 8: Factor the Velocity Equation
Factoring this quadratic equation:
(v−3)(v+1)=0
Step 9: Solve for Velocity
Setting each factor to zero gives us the possible values for v:
1. v−3=0 → v=3m/s
2. v+1=0 → v=−1m/s
Since we are interested in maximum velocity, we take:
Vmax=3m/s
Conclusion
From the analysis, we conclude:
- The amplitude of oscillation is 1meter.
- The maximum velocity is 3m/s.
Thus, the correct statements are options 1 and 2.
We start by substituting the total energy into the equation:
At the extreme position of oscillation, the velocity v is zero. Thus, we can simplify the equation:
3=x2+2x
Rearranging gives us:
Next, we can factor this quadratic equation:
Setting each factor to zero gives us the possible values for x:
2. x−1=0 → x=1
To find the maximum velocity, we analyze the total energy at the mean position (where x=0). Substituting x=0 into the energy equation:
3=v2−2v
Rearranging gives us:
Factoring this quadratic equation:
Setting each factor to zero gives us the possible values for v:
2. v+1=0 → v=−1m/s
From the analysis, we conclude:
- The maximum velocity is 3m/s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Matrix matching type questions
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:JEE Advanced
Explore 34 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Passage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is
View SolutionIn SHM, match the following.

View SolutionA particle moves such that its acceleration is given by a=−β(x−2)
Here, β is a positive constnt and x the x-coordinate with respect to the origin. Time period of oscillation is
View SolutionWhen an electric field is applied across a semiconductor,
View SolutionIf a machine perform 4000 J output work and 1000 J is inside loss due to friction , then the find efficiency?
View SolutionThe velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is V(x)=k|x|3 where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View SolutionTotal energy of a particle executing oscillating motionis 3 joule and given by E=x^(2)+2x +v^(2)-2v Where x is the displacement from origin at x=0 and v is velocity of particle at x. Then choose the correct statements)
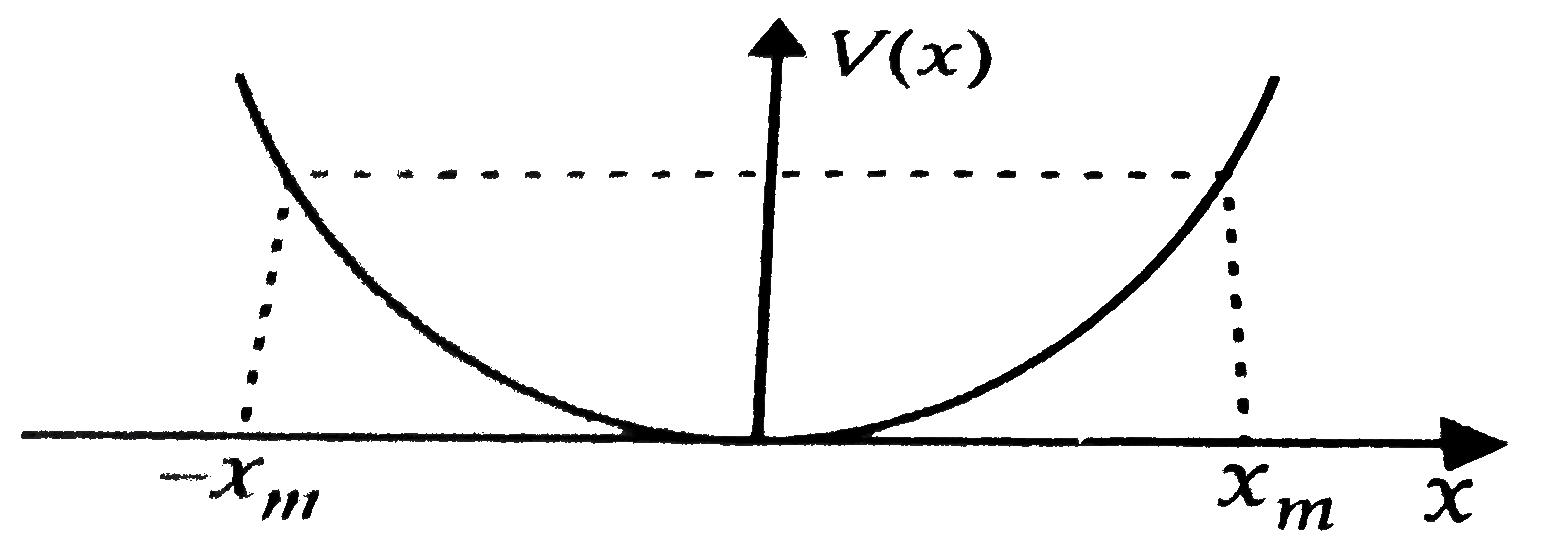
View SolutionThe potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
View SolutionDisplacment x of a particle at time t is given by x=At2+Bt+C, where A,B,Care constants .If v is its velocity, then :4Ax−v2=
View SolutionDispalcement (x) and velocity (v) of a particle exectuting S.H.M are related as 2v^(2)=9-x^(2) . The time period of particle is
View SolutionThe velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
View SolutionThe total energy of a particle, executing simple harmonic motion is : (x is displacement of the particle)
View SolutionThe potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?

View Solution
