Trajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

The correct Answer is:A→r,B→r,C→p,D→q
Comparing with the standard equation of projectile,
y=xtanθ−gx22u2cosθ
We get, θ=45∘ and u=20√2ms−1
Time period of this projectile is 4s. Hence, after 4s, velocity vector will again make and angle of 45∘ with horizontal.
So, maximum height, h=u2sin2θ2g=(20√2)2sin2(45∘)2×10
H=400×2×1220=40020=20m
and horizontal range, R=u2sin2θg=(20√2)2sin2(45∘)10
=400×2×110(∵sin90∘=1)
⇒R=80m
Similar Questions
Trajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
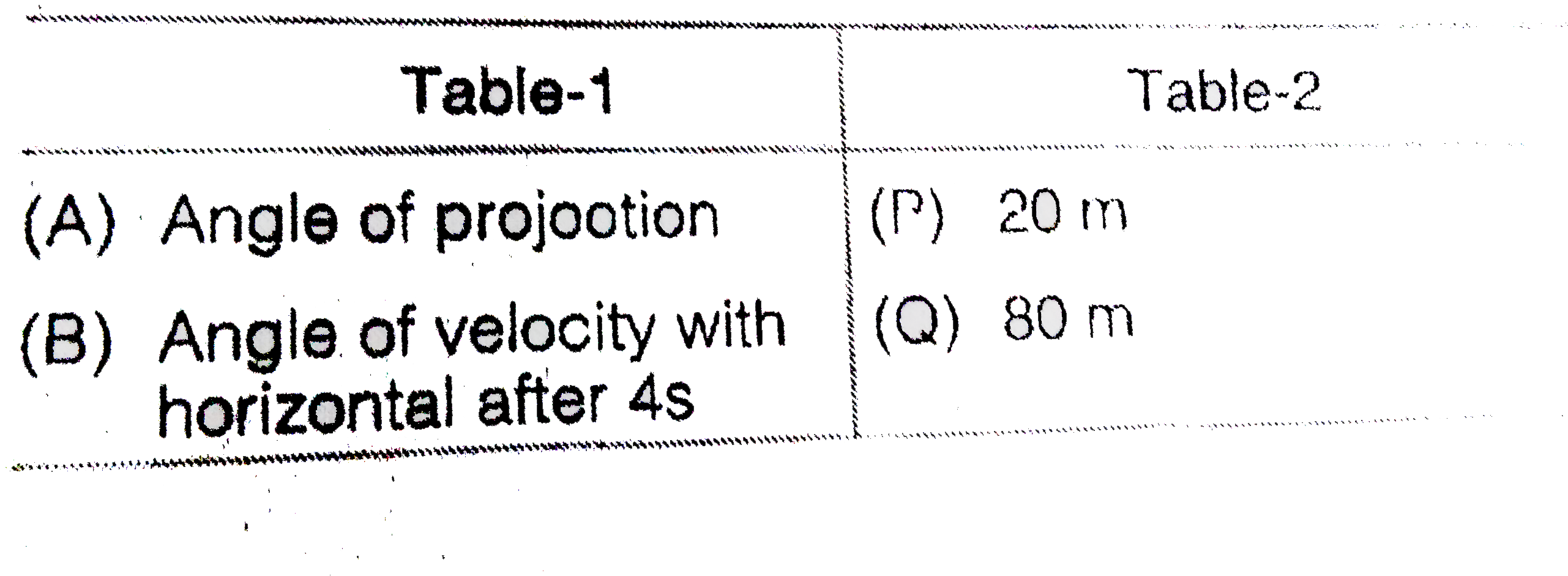
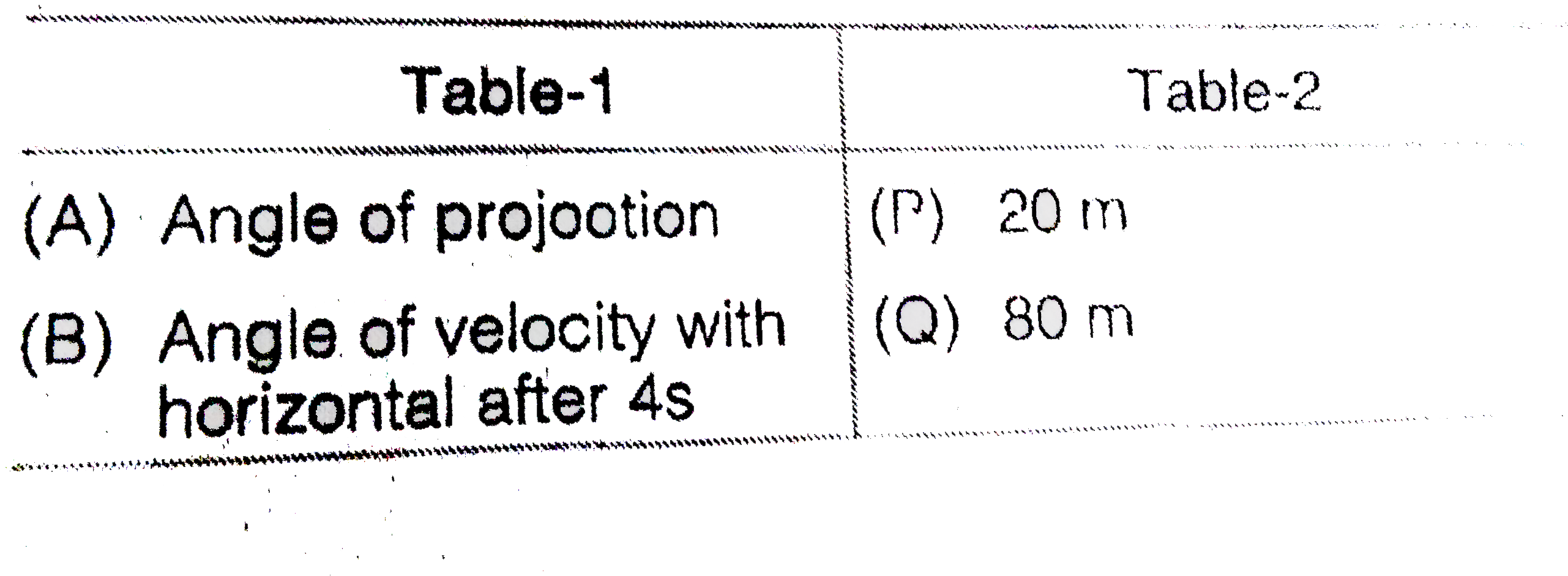
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
View Solution
Knowledge Check
In the projectile motion shown is figure, given tAB=2sthen(g=10ms−2)
 Aparticle is at point B at 3 sBmaximum height of projectile is 20 mCinitial vertical component of velocity is 20ms−1Dhorizontal component of velocity is 20ms−1
Aparticle is at point B at 3 sBmaximum height of projectile is 20 mCinitial vertical component of velocity is 20ms−1Dhorizontal component of velocity is 20ms−1A motion is described by y=3ex.e−3t where y,x are in metre and t is in second :
AThis represents equation of progressive wavepropagating along - X direction with 3ms−1BThis represents equation of progressive wave propagating along + X direction with 3ms−1CThis does not represent a progressive wave equationDData is insufficient to arrive at any conclusion ofthis shortIf y=x−x2 is the path of a projectile, then which of following is incorrect (g=10m/s2):
ARange =1mBTime of flight =5secCMaximum height =0.25 mDAngle of projectile =45∘
Trajectory of particle in a projectile motion is given as: y=x−(x2/80) (x and y are in meters). Take g=10m/s2.

View SolutionTrajectory of particle in projectile motion is y=(x−x2/80), x and y are in metre.
Projectile range is on horizontal plane.

View SolutionTrajectory of a particle in a projectile motion is given by y=x−x280 where x and y are in meters. Match the column-1 and column-2.
Column-IColumn-II(A)x coordinate at height of 15 m(P) 20 m(B)vertical distnce of particle frompoint of projection at x= 100 m(Q) 80 m(C)Horizontal range(R) 60 m(S) 25 m
View SolutionTrajectory of a projectile is given by y=αx+βx2. Then find (α+β).
View SolutionThe potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View Solution
