Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
3m1m2m1+m2g
m1+m24m1m2g
2m1m2m1+m2g
m1m2m1+m2g
The correct Answer is:A
To find the tension in the string connecting two masses m1 and m2 over a frictionless, massless pulley that is accelerating upwards with an acceleration of g2, we can follow these steps:
Step 1: Identify the Forces Acting on Each Mass
1. For mass m1 (which is lighter):
- Weight acting downwards: m1g
- Tension T acting upwards.
- Since the pulley is accelerating upwards, the effective acceleration acting on m1 is g2 upwards.
The net force equation for m1 can be written as:
T−m1g=−m1(g2)
(The negative sign indicates that the acceleration is upwards against the weight.)
2. For mass m2 (which is heavier):
- Weight acting downwards: m2g
- Tension T acting upwards.
- The effective acceleration acting on m2 is also g2 upwards.
The net force equation for m2 can be written as:
m2g−T=m2(g2)
Step 2: Set Up the Equations
From the equations derived from the forces acting on m1 and m2:
1. For m1:
T−m1g=−m1g2(1)
2. For m2:
m2g−T=m2g2(2)
Step 3: Solve the Equations
From equation (1):
T=m1g−m1g2=m1g2(3)
From equation (2):
T=m2g−m2g2=m2g2(4)
Step 4: Equate the Two Expressions for Tension
From equations (3) and (4):
m1g2=m2g−m2g2
Step 5: Simplify and Solve for Tension
Combine and simplify:
m1g2+m2g2=m2g
(m1+m2)g2=m2g
This leads to:
T=m1g+m2g2=(m1+m2)g2
Final Expression for Tension
Thus, the tension T in the string is given by:
T=(m1+m2)g2
1. For mass m1 (which is lighter):
- Weight acting downwards: m1g
- Tension T acting upwards.
- Since the pulley is accelerating upwards, the effective acceleration acting on m1 is g2 upwards.
The net force equation for m1 can be written as:
T−m1g=−m1(g2)
(The negative sign indicates that the acceleration is upwards against the weight.)
- Weight acting downwards: m2g
- Tension T acting upwards.
- The effective acceleration acting on m2 is also g2 upwards.
The net force equation for m2 can be written as:
m2g−T=m2(g2)
From the equations derived from the forces acting on m1 and m2:
T−m1g=−m1g2(1)
m2g−T=m2g2(2)
From equation (1):
T=m1g−m1g2=m1g2(3)
T=m2g−m2g2=m2g2(4)
From equations (3) and (4):
m1g2=m2g−m2g2
Combine and simplify:
m1g2+m2g2=m2g
(m1+m2)g2=m2g
This leads to:
T=m1g+m2g2=(m1+m2)g2
Thus, the tension T in the string is given by:
T=(m1+m2)g2
Similar Questions
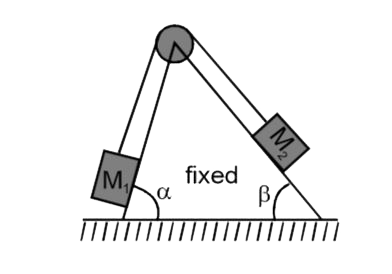
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses m_(1) and m_(2) are connected to the ends of string passing over a pulley. Find the tension and the acceleration associated.
View SolutionFind the relation between acceleration of the two blocks m_(1) and m_(2) . Assume pulleys are massless and frictionless and the strings are inextensible .
View Solutionदो द्रव्यमान m1, तथा m2(m1>m2) द्रव्यमानहीन तथा अवितान्य डोरी से परस्पर जुड़े हुये हैं, जो कि एक भारहीन तथा घर्षणरहित घिरनी से होकर जाती है। निकाय के द्रव्यमान केन्द्र का त्वरण होगा
View SolutionA massless string passes over a frictionless pulley and carries mass m_(1) hanging at one end and mass m_(2) connected by another massless string to mass m_(3) at other end as shown in figure . Calculate the tension in string joining masses m_(2)"and " m_(3) .
View SolutionTwo unequal masses m1 and m2 are connected by a string which passes over a frictionless and massless pulley. Find the tension in the string and the acceleration of the masses.
View SolutionTwo bodies of masses m_(1) " and " m_(2) are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration (g)/(2) , then tension in the string will be
View Solution

