Two cells of emf E1=6V and E2=5 are joined in parallel with same polarity on same side without any external load. If their internal resistance are r1=2Ω and r2=3Ω respectively, then
terminal potentiasl difference across any cell is less than 5V
terminal potential differences any cell is 5.6V
current through the cells is 0.2A
current through the cells is zero if E1=E2
The correct Answer is:B, C, D
To solve the problem step by step, we will use Kirchhoff's voltage law (KVL) and the concepts of internal resistance in parallel circuits.
Step 1: Understand the Circuit Configuration
We have two cells connected in parallel:
- Cell 1 with emf E1=6V and internal resistance r1=2Ω
- Cell 2 with emf E2=5V and internal resistance r2=3Ω
Step 2: Apply Kirchhoff's Voltage Law (KVL)
To find the current flowing through the circuit, we can apply KVL to the loop formed by the two cells. We assume a current I flows through the circuit.
Starting from one point in the loop (let's call it point A) and going around the loop, we can write the KVL equation:
E1−Ir1−E2−Ir2=0
This simplifies to:
E1−E2=I(r1+r2)
Step 3: Substitute the Values
Substituting the given values into the equation:
6V−5V=I(2Ω+3Ω)
1V=I(5Ω)
Step 4: Solve for Current I
Now, we can solve for I:
I=1V5Ω=0.2A
Step 5: Calculate Terminal Potential Difference for Cell 1
To find the terminal potential difference across cell 1, we can use the formula:
VAB=E1−Ir1
Substituting the values:
VAB=6V−(0.2A×2Ω)=6V−0.4V=5.6V
Step 6: Calculate Terminal Potential Difference for Cell 2
Similarly, for cell 2, we can use:
VCD=E2+Ir2
Substituting the values:
VCD=5V+(0.2A×3Ω)=5V+0.6V=5.6V
Summary of Results
- Current flowing through the circuit I=0.2A
- Terminal potential difference across cell 1 VAB=5.6V
- Terminal potential difference across cell 2 VCD=5.6V
We have two cells connected in parallel:
- Cell 1 with emf E1=6V and internal resistance r1=2Ω
- Cell 2 with emf E2=5V and internal resistance r2=3Ω
To find the current flowing through the circuit, we can apply KVL to the loop formed by the two cells. We assume a current I flows through the circuit.
E1−Ir1−E2−Ir2=0
This simplifies to:
E1−E2=I(r1+r2)
Substituting the given values into the equation:
6V−5V=I(2Ω+3Ω)
1V=I(5Ω)
Now, we can solve for I:
I=1V5Ω=0.2A
To find the terminal potential difference across cell 1, we can use the formula:
VAB=E1−Ir1
Substituting the values:
VAB=6V−(0.2A×2Ω)=6V−0.4V=5.6V
Similarly, for cell 2, we can use:
VCD=E2+Ir2
Substituting the values:
VCD=5V+(0.2A×3Ω)=5V+0.6V=5.6V
- Current flowing through the circuit I=0.2A
- Terminal potential difference across cell 1 VAB=5.6V
- Terminal potential difference across cell 2 VCD=5.6V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Single Correct
26 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be ast 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The voltmeter reading will be
View SolutionFind the equivalent resistance of the triangular bipyramid between the points.

a. A and C , b. DandE
View SolutionTwo cells A and B of emf 1.3V and 1.5Vrespectively are arranged as shown in figure. The voltmeter reds 1.45V. The voltmeter is assumed to be ideal. Then

View SolutionThe LC product of a tuned amplifier circuit require to generate a carrier wave of 1 MHz for amplitude modulation is
View SolutionA long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4×10−3Wb. The self-inductance of the solenoid is
View SolutionIn the circuit shown in figure E_1=7V,E_2=1 V,R_1=2Omega, R_2=2Omega and R_3=3Omega respectively. Find the power supplied by the two batteries.
View SolutionTwo cells of emf E1=6V and E2=5 are joined in parallel with same polarity on same side without any external load. If their internal resistance are r1=2Ω and r2=3Ω respectively, then
View SolutionFor the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
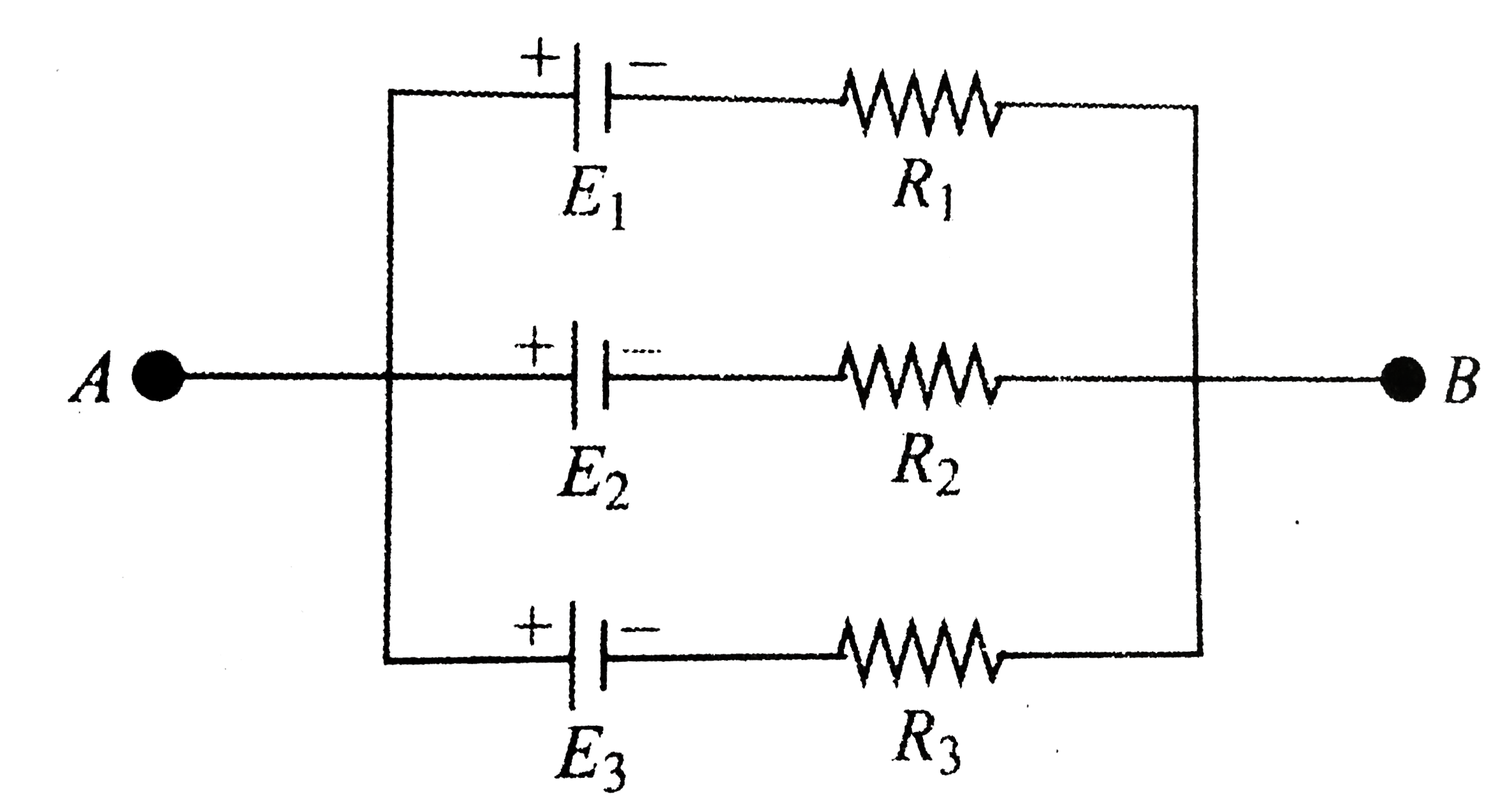
View SolutionE_1,E_2 and r_1,r_2 are respectively. The emf's and internal resistances of two cells. The current through an external resistance R when it is connected to the first cell is equal to that when it is connected to the second. Here, the probable relations are
View SolutionTwo cells of emf E1.E2 and internal resistance r1,r2 respectively are connected to parallel combination. Determine the equivalent emf of the combination.
View SolutionTwo similar cells, whether joined in series or in parallel, have the same current through an external resistance of 2Ω . The internal resistance of each cell is :
View SolutionA cell to emf. E and internal resistance r supplies currents for the same time t through external resistance R_1 and R_2 respectively. If the heat produced in both cases is the same, then the internal resistance is given by :
View SolutionTwo cells of emf E_1 and E_2 and internal resistance r_1 and r_2 are connected in parallel such that they send current in same direction. Derive an expression for equivalent resistance and equivalent emf of the combination.
View SolutionTwo cells of emf E_1 and E_2 having internal resistance r _1 and r_2 are connected in parallel. Calculate Eeq and req for the combination.
View SolutionLet two cells of e.m.f.'s E1andE2 be connected in parallel in a circuit . Let r1andr2 be the internal resistances of the cells . Find the value of the current
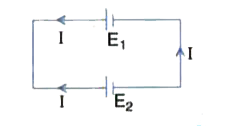
View Solution

