Two charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
Step by step video solution for Two charges q_(1) and q_(2) are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.2
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two charges −q each are separated by distance 2d. A third charge +q is kept at mid-point O. Find potential energy of +q as a function of small distance x from O due to −q charges. Prove that the charge at O is in an unstable equilibrium.
View SolutionIn the figure shown a conducting sphere of inner radius 'a' and outer radius 'b' is given a charge Q. A point charge 'q' is placed in the cavity of this sphere at distance 'x'(<a) away from the centre. Find the electric field intensity and electric potentials at point P (outside the sphere) at distance r>b. Also find the electric potential at point C

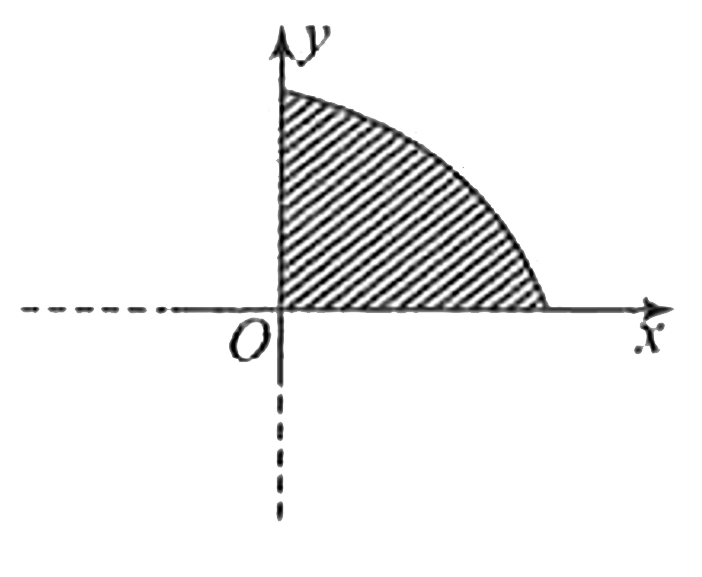
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
View SolutionElectric flux through a surface are 10m2 lying in the xy plane is (if→E=ˆi+√2ˆj+√3ˆkN/C)
View SolutionThe measurement of an unknown resistance R is to be carried out using Wheatstone bridge (see Fig. 2(EP).3). Two students perform an experiment in two way. The first student takes R2=10Ω and R1=5Ω. The other student takes R2=1000Ω and R1=500Ω. In the standard arm, both take R3=5Ω. Both find R=R2R1R3=10Ω within errors.
View SolutionIf the points (0,0),(3,3),(p,q) form an equilateral triangle and q_(1),q_(2) are the two values of q then q_(1)+q_(2)=
View SolutionTwo charges q_(1) and q_(2) are placed at (0,0,d) and (0,0,-d) respectively. Find icons of points where the potential is zero.
View SolutionTwo charges q1andq2 are placed at (0,0d)and(0,0−d) respectively. Find locus of points where the potential is zero.
View SolutionThe point charges q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at origin.
View SolutionTwo charges q_(1) and q_(2) are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View SolutionTwo point charges of magnitude +q and -q are placed at (−d2,0,0) and (d2,0,0) respectively. Find the equation of the equipotential surface where the potential is zero.
View SolutionA system has two charges qA=2.5×10−7C and qB=−2.5×10−7C located at points A≡(0,0,−15cm) and B=(0,0,+15cm)respectively. What are the total charge and electric dipole moment of the system?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges of magnitude + q and - q are placed at (-(d)/(2),0,0) and ((d)/(2),0,0) . respectively. Find the equation of the equipotential surface where the potential is zero.
View SolutionTwo charges q1 and q2 are placed at (0, 0, d) and (0, 0, - d) respectively. Find locus or points where the potential is zero.
View Solution

