Two circular discs A and B of equal masses and thicknesses. But are made of metals with densities dAanddB(dA>dB). If their moments of inertia about an axis passing through the centre and normal to the circular faces be IAandIB, then.
IA=IB
IA>IB
IA<IB
IA≥IB
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the moments of inertia of two circular discs made of different materials but having equal masses and thicknesses.
1. Understanding the Given Information:
- We have two circular discs, A and B.
- Both discs have equal masses (m) and equal thicknesses (t).
- The densities of the discs are different, with dA>dB.
2. Relating Mass and Density:
- The mass of each disc can be expressed in terms of its density and volume. The volume V of a circular disc is given by:
V=πr2t
- Therefore, the mass m of each disc can be written as:
m=d⋅V=d⋅(πr2t)
- For disc A:
mA=dA⋅(πr2At)
- For disc B:
mB=dB⋅(πr2Bt)
3. Setting the Masses Equal:
- Since the masses are equal:
dA⋅(πr2At)=dB⋅(πr2Bt)
- We can simplify this to:
dAr2A=dBr2B
4. Calculating the Moment of Inertia:
- The moment of inertia I of a disc about an axis through its center and normal to its face is given by:
I=12mr2
- For disc A:
IA=12mAr2A=12(dA⋅πr2At)r2A=12dA⋅πtr4A
- For disc B:
IB=12mBr2B=12(dB⋅πr2Bt)r2B=12dB⋅πtr4B
5. Expressing r2A and r2B:
- From the mass equality derived earlier:
r2A=dBdAr2B
- Substitute this into the expressions for IA and IB:
IA=12dA⋅πt(dBdAr2B)2=12dA⋅πt⋅d2Bd2Ar4B
- Thus:
IA=12⋅d2BdA⋅πtr4B
6. Comparing IA and IB:
- Now we can compare IA and IB:
IB=12dB⋅πtr4B
- Since dA>dB, we can conclude:
IA<IB
Conclusion:
Thus, the moment of inertia of disc A is less than that of disc B:
IA<IB
- We have two circular discs, A and B.
- Both discs have equal masses (m) and equal thicknesses (t).
- The densities of the discs are different, with dA>dB.
- The mass of each disc can be expressed in terms of its density and volume. The volume V of a circular disc is given by:
V=πr2t
- Therefore, the mass m of each disc can be written as:
m=d⋅V=d⋅(πr2t)
- For disc A:
mA=dA⋅(πr2At)
- For disc B:
mB=dB⋅(πr2Bt)
- Since the masses are equal:
dA⋅(πr2At)=dB⋅(πr2Bt)
- We can simplify this to:
dAr2A=dBr2B
- The moment of inertia I of a disc about an axis through its center and normal to its face is given by:
I=12mr2
- For disc A:
IA=12mAr2A=12(dA⋅πr2At)r2A=12dA⋅πtr4A
- For disc B:
IB=12mBr2B=12(dB⋅πr2Bt)r2B=12dB⋅πtr4B
- From the mass equality derived earlier:
r2A=dBdAr2B
- Substitute this into the expressions for IA and IB:
IA=12dA⋅πt(dBdAr2B)2=12dA⋅πt⋅d2Bd2Ar4B
- Thus:
IA=12⋅d2BdA⋅πtr4B
- Now we can compare IA and IB:
IB=12dB⋅πtr4B
- Since dA>dB, we can conclude:
IA<IB
Thus, the moment of inertia of disc A is less than that of disc B:
IA<IB
टॉपर्स ने हल किए ये सवाल
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
12 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
समान प्रश्न
A rigid body is in pure rotation, that is, undergoing fixed axis rotation. Then which of the following statement(s) are true?
View SolutionA uniform rod of mass M=2kg and length L is suspended by two smooth hinges 1 and 2 as shown in Fig. A force F=4N is applied downward at a distance L/4 from hinge 2. Due to the application of force F, hinge 2 breaks. At this instant, applied force F is also removed. The rod starts to rotate downward about hinge 1. (g=10m/s2)

The reaction at hinge 1, before hinge 2 breaks, is
View SolutionIn the instant shown in the diagram the board is moving up (vertically) with velocity v. The drum winds up at a constant rate ω. If the radius of the drum is R and the board always remains horizontal, find the value of velocity in terms of R,θ,ω.

View SolutionTwo soap bubbles A and B are kept in aclosed chamber where the air is maintained at pressure 8Nm2. The radiiof bubbles A and B are 2cm and 4 cm , respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. The ratio of nB/nAis ( where nA and nB are the numbe of moles of air in bubbles A and B,respectively.)
[Neglect the effect of gravity]
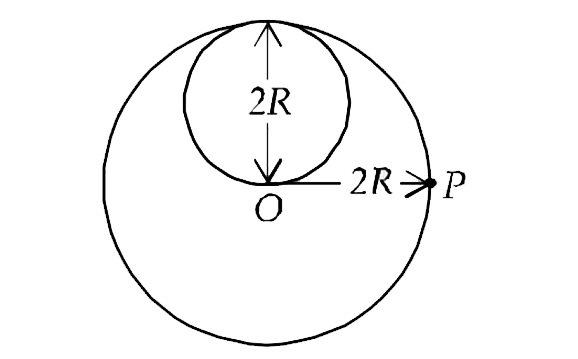
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO is
View SolutionOne solid sphere A and another hollow spher B are of same mass and same outer radii. Their moment of inertia aobut their diameters are respectively I_A and I_B such that where d_A and d_B are their densities,
View SolutionTwo circular discs A and B of equal masses and thicknesses. But are made of metals with densities dAanddB(dA>dB). If their moments of inertia about an axis passing through the centre and normal to the circular faces be IAandIB, then.
View SolutionThe moments of inertia of two rotating bodies A and are IA and IB(IA>IB). If their angular momenta are equal then.
View SolutionTwo circular disc of same mass and thickness are made from metals having densities rho_(1) and rho_(2) respectively. The ratio of their moment of inertia about an axis passing through its centre is,
View SolutionA and B are isotopes. B and C are isobars. If dA,dB and dC be the densities of nuclei A, B and C respectively then
View SolutionMoment of inertia of a circular ring of mass m and radius r about the normal axis passing through its centre is
View SolutionThe moment of inertia of a circular disc of mass m and radius r about an perpendicular axis passing through its centre is
View SolutionThe moment of inertia of circular disc about its diameter is 200 g cm^(2) . Then its moment of inertia about an axis passing through its centre and normal to its face is :
View SolutionT_AK A standard gas concentration in temperature d_A And T_BK B is the concentration of the ideal gas in warming d_B . If the molecular mass of A gas is 4 times that of B gas and T_A : T_B = 2 : 1 Oh d_A : d_B = 1 : 2 Yes, but A and B gas pressure ratio:
View Solutionদুটি মৌল A ও B যথাক্রমে দেহকেন্দ্রিক ও পৃষ্ঠকেন্দ্রিক ঘনকাকার কেলাস গঠন করে। A ও B -এর ঘনত্ব যথাক্রমে d_A ও d_B এবং পারমাণবিক ভর যথাক্রমে M_A, ও M_B । যদি উভয় কেলাসের বাহুর দৈর্ঘ্য সমান হয় এবং d_A>d_B হয়,তবে M_Aও M_B-এর কোনটি বেশি?
View Solution

