Two concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1>>r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
Suppose a current I2 flows through the outer circular coil. The field at the centre of the coil is
B2=μ0I22r2
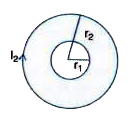
The second co-axially placed coil has very small radius. So B2 may be considered constant over its cross-sectional area
Now, ϕ1=πr21B2=πr21(μ0I22r2)
or ϕ1=μ0πr212r2I2
Comparing with ϕ=M12I2, we get
M12=μ0πr212r2
Also, M21=M12=μ0πr212r2
It would have been difficult to calculate the flux through the bigger coil of the non-uniform field due to the current in the smaller coil and hence the mutual inductance M12. The equality M12=M21 is helpul. Note also that mutual inductance depends solely on the geometry.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Long Answer Questions)
1 Video
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Short Answer Questions)
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
12 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
State Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View SolutionA current -carrying loop of irregular shape is located in an external magnetic field. If the wire is flexible, why does it becomes circular?
View SolutionCurrent in a coil increases from 0 to 1 ampere in 0.1 second. If self inductance of the coil is 5 millihenry, magnitude of induced emf is
View SolutionA metal sphere with its centre at A and radius R has a charge 2q on it. The field at a point B outside the sphere is E. If another metal sphere of radius 3R and having a charge -3q is placed with its centre at point B, find out the resultant electric field at a point mid way between A and B.
View SolutionA parallel plate capacitor consists of two circular plates each of radius 2cm, separated by a distance of 0.1mm. If the potential difference across the plates is varying at the rate of 5×106Vs−1, then the value of displacement current is
View SolutionIn co-axial concentric coils of radius r_(1) and r_(2) such that r_(1) lt lt r_(2) Fig. find direction of induced current when K is (i) pressed (ii) released.
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r_(1) and the other of radius r_(2)(r_(1) lt r_(2)) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement. (b) A rectangular coil of area A , having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B , the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2pifNBA .
View Solutionदो संकेद्रीय (concentric ) वृत्ताकार कुंडलियाँ समाक्षीय रुप से (coaxially) व्यवस्थित हैं । इनकी त्रिज्याएँ r1 तथा (r2 हैं तथा r1≤≤r2 हैं । इस अवस्था का अन्योन्य प्रेरकत्व (mutual inductance) ज्ञात करें ।

View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solutionदो संकेंद्रित वृताकार कुंडलिया एक कम त्रिजिया r1 की तथा दूसरी अधिक त्रिजिया r2 की ऐसे की r1>>r2 समाक्षी रखी है था दोनों के केंद्र संपत्ति है इस व्यवस्था के लिए अन्यों परिकत्व ज्ञात कीजिये
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo circular coils, one of smaller radius r_(1) and the other of very large radius r_(2) are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo concentric circular coils, one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.

View Solution

