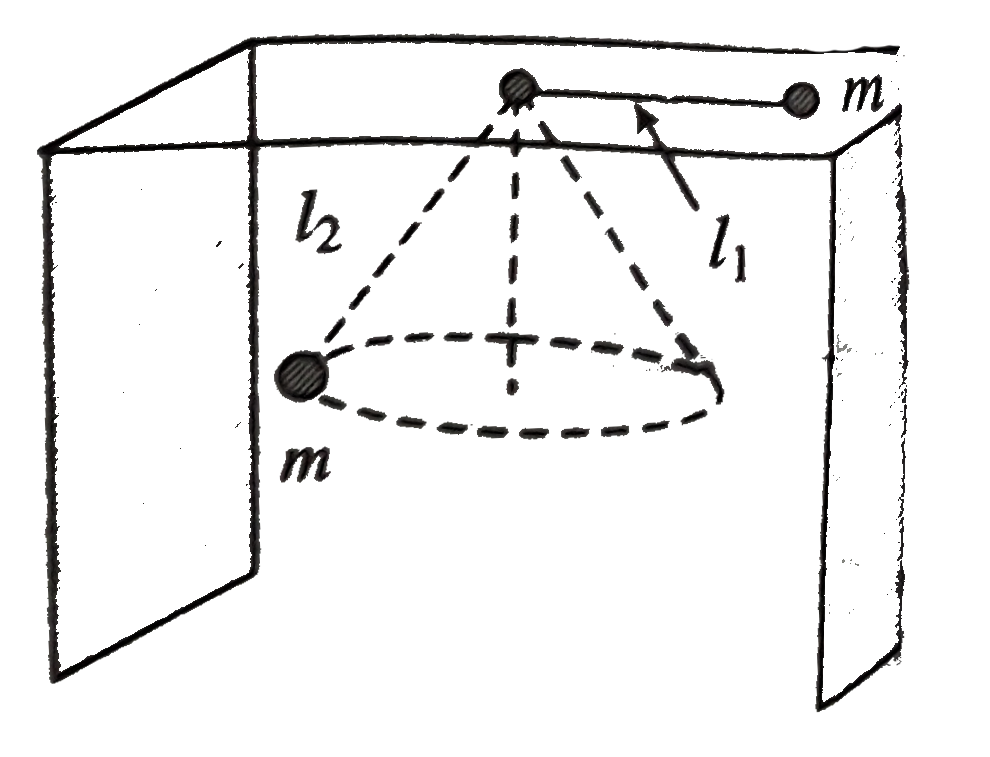
Two identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity ω1 and the ther is made a move is a horizontal ω2 if l1and l2 are the length the table , than in order that particle under down the table neither moves down nor move up the ratiol1/l2 is
ω1ω2
ω2ω1
ω21ω22
ω22ω21
The correct Answer is:d
T=mω21l1 …(i)
Tsinθ=mω22l2sinθ⇒T=mω22l2…(ii)
⇒l1l2=ω22ω21
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple Correct
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Linked Comprehension
Explore 52 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Subjective
Explore 21 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
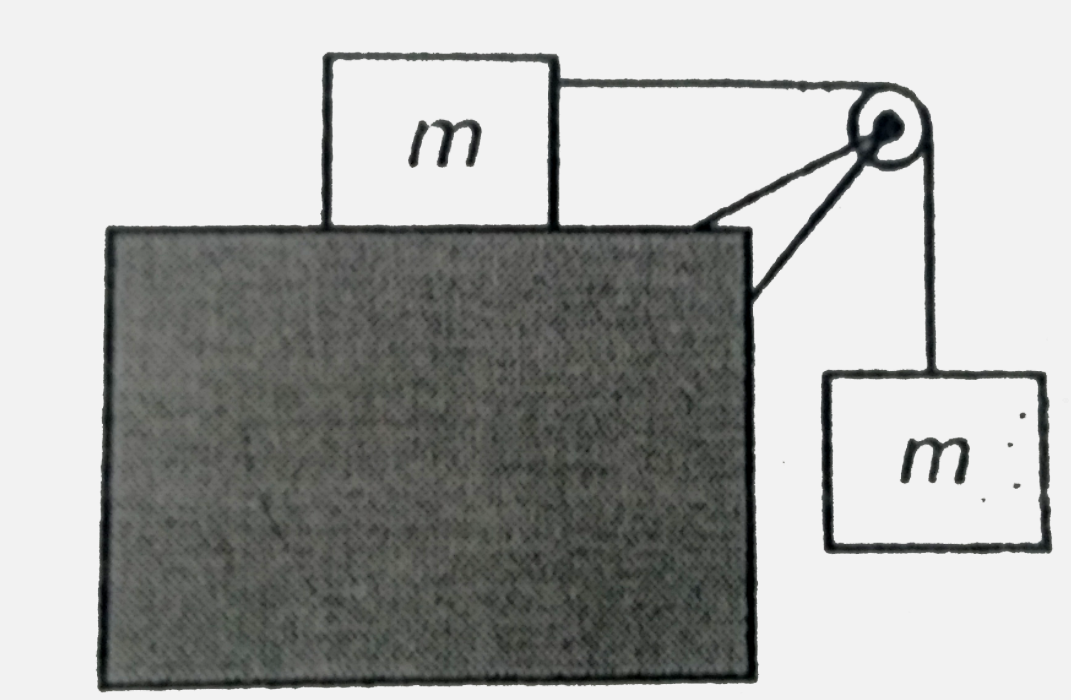
Two identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
View SolutionA particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
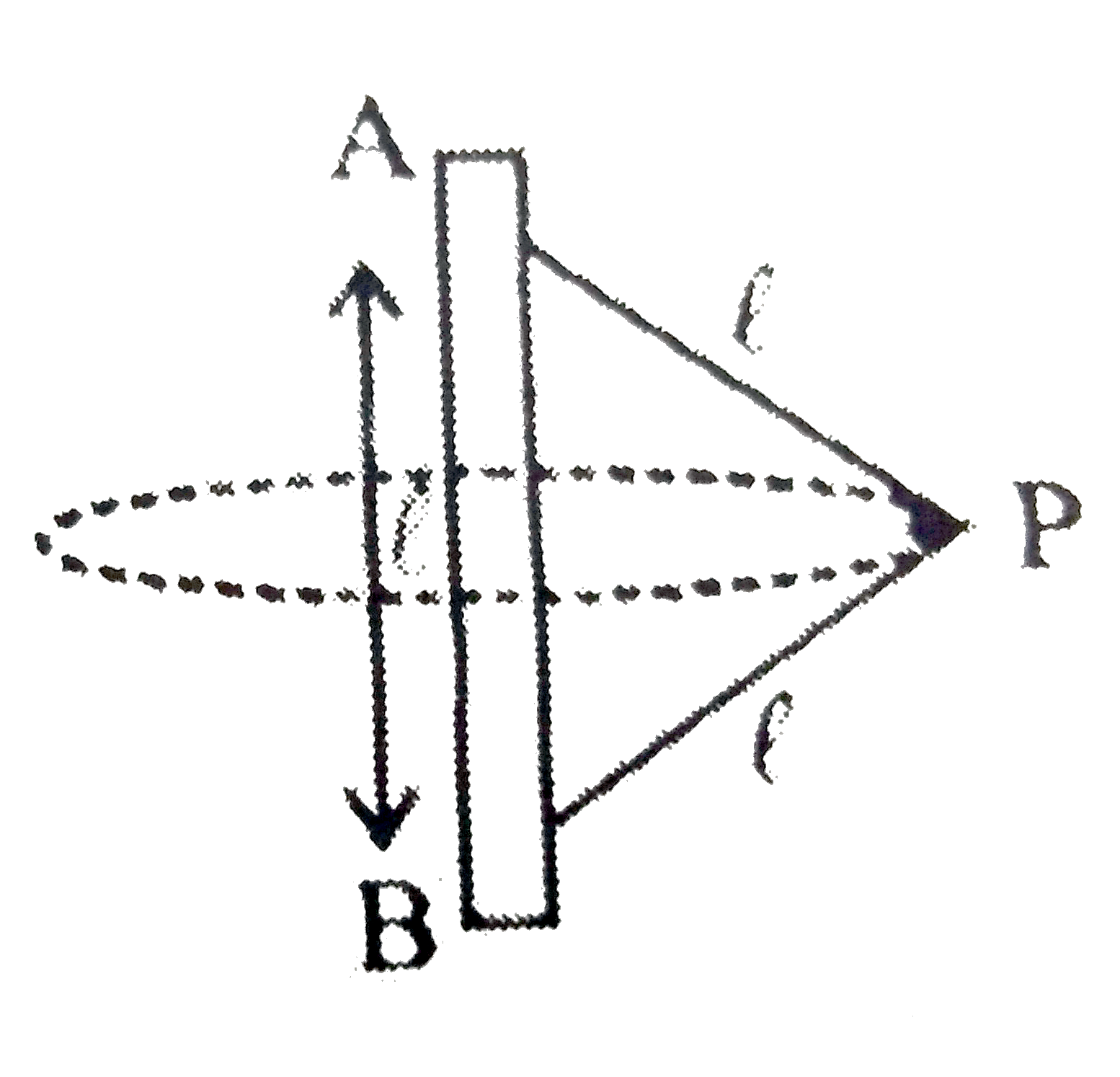
View SolutionA particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionTwo particles move on a circular path (one just inside and the other just outside) with the angular velocities ω and 5ω starting from the same point. Then
View SolutionTwo particles move on a circular path (one just inside and the other just outside) with the angular velocities ω and 5ω starting from the same point. Then
View Solution
