Two identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
π216
π28√2
( pi^(2))/(8)
π216√2
The correct Answer is:B
To find the ratio of the magnetic fields BA and BB at the centers of the circular and square wire configurations, we will follow these steps:
Step 1: Determine the magnetic field BA at the center of the circular wire
1. The length of wire A is given as L.
2. When bent into a circle, the radius R can be expressed as:
R=L2π
3. The formula for the magnetic field at the center of a circular loop carrying current I is:
BA=μ0I2R
4. Substituting the expression for R into the formula:
BA=μ0I2⋅L2π=μ0I⋅πL
Step 2: Determine the magnetic field BB at the center of the square wire
1. The length of wire B is also L.
2. When bent into a square, each side a can be expressed as:
a=L4
3. The magnetic field at the center of a square loop can be calculated using the formula:
BB=μ0I4π⋅(4⋅1√2⋅1a2)
where 1a2 accounts for the distance from the center to the midpoint of a side.
4. Substituting a=L4:
BB=μ0I4π⋅(4⋅1√2⋅2L/4)
5. Simplifying this expression:
BB=μ0I4π⋅(4⋅8L√2)=8μ0I4πL√2=2μ0IπL√2
Step 3: Calculate the ratio BABB
1. Now we can find the ratio of the magnetic fields:
BABB=μ0I⋅πL2μ0IπL√2
2. Simplifying this ratio:
BABB=μ0I⋅πL⋅πL√22μ0I=π2√22
Final Result
Thus, the ratio of the magnetic fields is:
BABB=π2√22
1. The length of wire A is given as L.
2. When bent into a circle, the radius R can be expressed as:
R=L2π
3. The formula for the magnetic field at the center of a circular loop carrying current I is:
BA=μ0I2R
4. Substituting the expression for R into the formula:
BA=μ0I2⋅L2π=μ0I⋅πL
1. The length of wire B is also L.
2. When bent into a square, each side a can be expressed as:
a=L4
3. The magnetic field at the center of a square loop can be calculated using the formula:
BB=μ0I4π⋅(4⋅1√2⋅1a2)
where 1a2 accounts for the distance from the center to the midpoint of a side.
4. Substituting a=L4:
BB=μ0I4π⋅(4⋅1√2⋅2L/4)
5. Simplifying this expression:
BB=μ0I4π⋅(4⋅8L√2)=8μ0I4πL√2=2μ0IπL√2
1. Now we can find the ratio of the magnetic fields:
BABB=μ0I⋅πL2μ0IπL√2
2. Simplifying this ratio:
BABB=μ0I⋅πL⋅πL√22μ0I=π2√22
Thus, the ratio of the magnetic fields is:
BABB=π2√22
Similar Questions
A current carrying thin uniform wire of length '4l' is bent like a square so that it produces a magnetic induction B_(1) at the centre of the square. When the same wire is bent like a circle, it produces a magnetic induction B_(2) at the centre of the circle. The ratio between B_(1) and B_(2) is
View Solutionदो एकसमान तार A व B , प्रत्येक लम्बाई l, में समान धारा I प्रवाहित है । A को मोड़कर त्रिज्या R का एक वृत्त और B को मोड़कर भुजा a का एक वर्ग बनाया जाता है । यदि BA तथा BB क्रमशः वृत्त के केंद्र तथा वर्ग के केंद्र पर चुम्बकीय क्षेत्र हैं , तो अनुपात (BABB) होगा :
View SolutionTwo indentical wires A and B, each of length I, carryi the same current I. Wire is bent into a circle of radius R and wire B is bent to form a square of side a. if B_(A) and B_(B) are the values of magnetic field at the centres of the circle and square respectively, thne the ratio B_(A)//B_(B) is
View SolutionFigures shows a long wire bent at the middle to form a right angle. The magnitudes of the magnetic fields at the points P, Q, R and S are B1,B2,B3,B4 respectively. The wire and the circumference of circle are coplanar. Relation between B1,B2,B3,B4 are
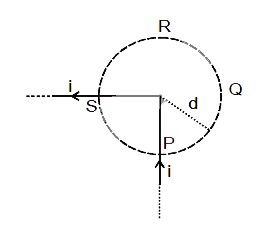
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionTwo identical wires A and B each of length 'l' carry the same current I wire A is bent into a circle of radius R and wire B is bent to form a square of side 'a' if B_a and B_b are the values of magnetic field at the centre of the circle and square respectively then the ration BABB is
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View Solution
