Two light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
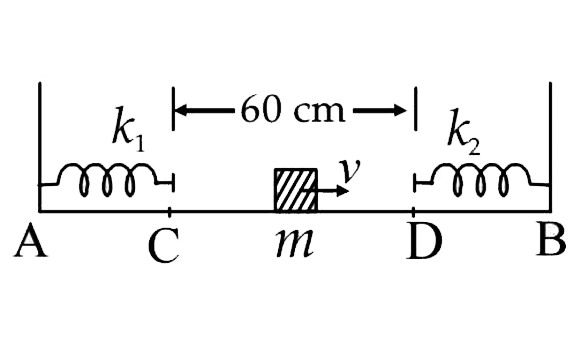 .
.
The correct Answer is:B, C
The mass will strike the right spring, compress it. The K.E. of the mass will convert into P.E. of the spring. Again the spring will return to its natural size thereby verting its P.E. to K.E. of the block.The time taken for this process will
beT2, where T=2pi sqrtm/k.
(##JMA_CHMO_C10_026_S01##).
:. t_(l) =T/2=pisqrtm/k_(2) =pisqrt(0/2)/(3.2)=0.785 sec<br>TheblockwillmoveomA→Bwithoutanyaee≤ration.<br>Thetimetakenwillbe<br>t_(2) =(60)/(120) =0.5<br>Nowtheblockwillcompressthe≤ftspr∈gandthenthespr∈gaga∈aa∈sitsnatural≤n>h.en>h.Thetimetakenwillbeoscillation.Thetimetakenfordo∈gso<br>t_(3)=pi sqrtm/k_(l) =pisqrt(0.2)/(1.8) =1.05 sec.<br>Aga∈theblockmovesomB→A,comp≤t∈o≠oscillation.Thetimetakenfordo∈gso<br>t_(4) =(60)/(120) =0.5<br>∴Thecomp≤tetimeofoscillationwillbe<br>=t_(l)+t_(2)+t_(3)+t_(4)<br>=0.785+0.51.05+05<br>=2.83(app.).
Similar Questions
Two light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
(##JMA_CHMO_C10_026_Q01##).
View SolutionTwo light spring of force constants k1andk2 and a block of mass m are in the line AB on a smooth horizontal table such that one end of each spring is fixed on right supports and the other and is free as shown in figure

The distance CD between the free ends of the spring is 60cm. If the block (k1=1.8N/m,k2=3.2N/mandm=200g). Is the motion simple harmonic?
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvkAn ideal spring is permanently connected between two blocks of masses M and m. The blocks-spring system can move over a smooth horizontal table along a straight line along the length of the spring as shown in Fig.The blocks are brought nearer to compress the spring and then released. In the subsequent motion,
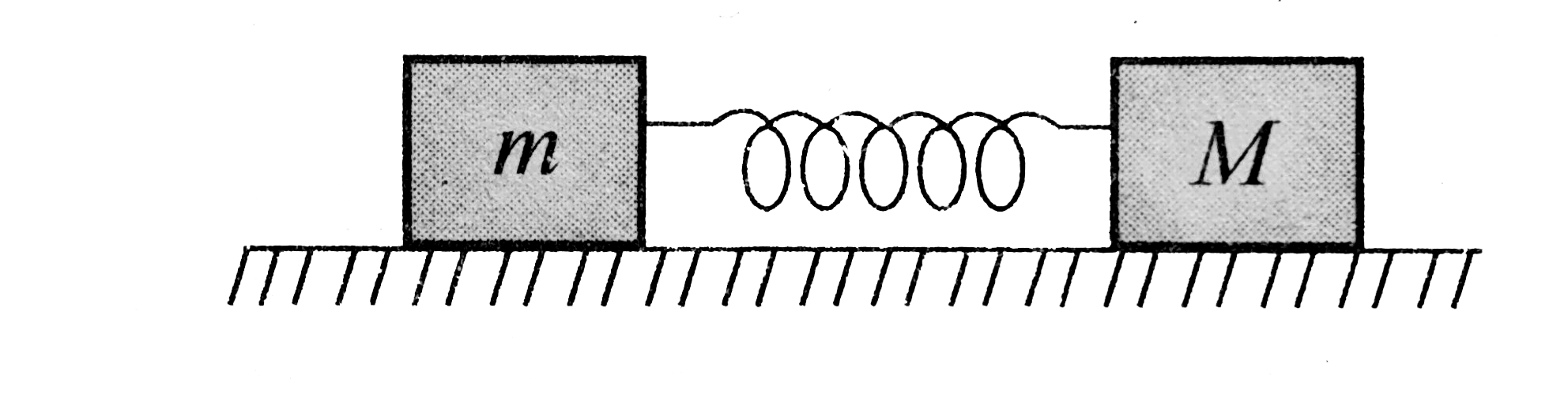 Ainitially they move in opposite directions with velocities inversely proportional to their massesBthe ratio of their velocities remains constantClinear momentum and energy of the system remain conservedDthe two blocks will Oscillate about their centre of mass which remains stationary
Ainitially they move in opposite directions with velocities inversely proportional to their massesBthe ratio of their velocities remains constantClinear momentum and energy of the system remain conservedDthe two blocks will Oscillate about their centre of mass which remains stationary
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution

