Two parallel long wires carry currents 18A and 3A. When the currents are in the same direction, the magnetic field at a point midway between the wire is B1. If the direction of i2 is reversed, the field becomes B2. Then the value of B1/B2 is
5:7
7:5
3:5
5:3
The correct Answer is:A
To solve the problem, we need to calculate the magnetic fields B1 and B2 at a point midway between two parallel wires carrying currents I1=18A and I2=3A.
1. Understanding the Magnetic Field due to a Current-Carrying Wire:
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ02πrI
where μ0 is the permeability of free space.
2. Calculating B1 when Currents are in the Same Direction:
When both currents are in the same direction, the magnetic fields due to both wires at the midpoint will add up. Therefore, the magnetic field B1 at the midpoint is:
B1=μ02πrI1−μ02πrI2
Substituting the values:
B1=μ02πr(I1−I2)=μ02πr(18−3)=μ02πr⋅15
3. Calculating B2 when Currents are in Opposite Directions:
When the direction of I2 is reversed, the magnetic fields will oppose each other. Therefore, the magnetic field B2 at the midpoint is:
B2=μ02πr(I1+I2)
Substituting the values:
B2=μ02πr(18+3)=μ02πr⋅21
4. Finding the Ratio B1B2:
Now we can find the ratio of B1 to B2:
B1B2=μ02πr⋅15μ02πr⋅21
The μ02πr terms cancel out:
B1B2=1521=57
5. Conclusion:
Therefore, the value of B1B2 is 57.
Final Answer:
B1B2=57
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ02πrI
where μ0 is the permeability of free space.
When both currents are in the same direction, the magnetic fields due to both wires at the midpoint will add up. Therefore, the magnetic field B1 at the midpoint is:
B1=μ02πrI1−μ02πrI2
Substituting the values:
B1=μ02πr(I1−I2)=μ02πr(18−3)=μ02πr⋅15
When the direction of I2 is reversed, the magnetic fields will oppose each other. Therefore, the magnetic field B2 at the midpoint is:
B2=μ02πr(I1+I2)
Substituting the values:
B2=μ02πr(18+3)=μ02πr⋅21
Now we can find the ratio of B1 to B2:
B1B2=μ02πr⋅15μ02πr⋅21
The μ02πr terms cancel out:
B1B2=1521=57
Therefore, the value of B1B2 is 57.
B1B2=57
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-II
Explore 79 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
A proton enters a magnetic field of flux density 1.5 T with a velocity of 2×107ms−1 at an angle of 30° with the field. The force on the proton is [ep=1.6×10−19C]
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionIn a sample of rock, the ratio of number of 206Pb to 238U nuclei is found to be 0.5. The age of the rock is (18/n)×109ln(32)ln2 year (Assume that all the Pb nuclides in he rock was produced due to the decay of Uranium nuclides and T1/2(238U)=4.5×109 year). Find n.
View SolutionTwo parallel, long wires carry current i1 and i2 withi1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 30μT. If the direction of i1 is reversed , the field becomes 90μT. The ratio i1/i2 is
View SolutionA wire of length L carrying current I is bent into a circle of one turn. The field at the center of the coil is B1. A similar wire of length L carrying current I is bent into a square of one turn. The field at its center is B2. Then (1) B_(1) gt B_(2) (2) B_(1) = B_(2) (3) (B_(1))/(B_(2))=2 (4) B_(1) lt B_(2)
View SolutionTwo long parallel straight conductors carry current i_(1) and i_(2)(i_(1)gti_(2)) . When the currents are in the same directions, the magnetic field at a point midway between the wires is 20muT . If the direction of i_(2) is reversed, the field becomes 50muT . The ratio of the current i_(1)//i_(2) is :
View SolutionTwo parallel long wire carry currents i_(1) and i_(2) with i_(1) gt i_(2) . When the currents are in the same direction , the magnetic field midway between the wires is 10 muT . When the direction of i_(2) is reversed, it becomes 40 muT . The ratio i_(1)//i_(2) is
View SolutionTwo parallel long wires carry currents i_(1) and i_(2) with i_(1) gt i_(2) .When the current are in the same direction, the magnetic field at a point midway between the wire is 20muT .If the direction of i_(1) ,is reversed.the field becomes 30muT .The ratio i_(1)//i_(2) is
View SolutionA current carrying thin uniform wire of length '4l' is bent like a square so that it produces a magnetic induction B_(1) at the centre of the square. When the same wire is bent like a circle, it produces a magnetic induction B_(2) at the centre of the circle. The ratio between B_(1) and B_(2) is
View SolutionA circular coil of radius r carries a current I . It produces magnetic fields B_(1) at the centre of the coil and B_(2) at an axial point at a distance r from the centre. The ratio of B_(1) and B_(2) is
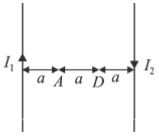
View SolutionTwo long parallel wires carry currents in opposite direction as shown. Points A and D lie in the same plane as the wires. The magnetic field at A and D is into the plane of the paper, with intensity BA and BD respectively. If BABD=75, the value of I1I2 is ____________________.
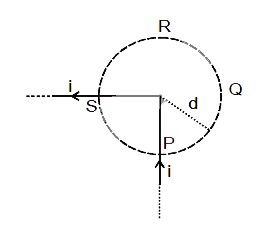
View SolutionFigures shows a long wire bent at the middle to form a right angle. The magnitudes of the magnetic fields at the points P, Q, R and S are B1,B2,B3,B4 respectively. The wire and the circumference of circle are coplanar. Relation between B1,B2,B3,B4 are
View SolutionTwo parallel, long wires carry currents t1andt2 with t1>t2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
View SolutionTwo long wires are placed parallel to each other. The current carried by these wires is, i1 and i2, respectively. Assume i1>i2. When current is flowing in the same direction then magnetic field midway between the two wires is 20μT. If direction of i2, is reversed then magnetic field at the same point becomes 60μT. What should be the ratio of currents?
View SolutionIf a square frame of side L is made from a uniform wire and current I is flowing through it and its magnetic field intensity at the centre is B_(1) . When the same current is passed through the circular loop whose circumference is same as that of the square, the magnetic field at the centre is B_(2) . What will be B_(1)//B_(2) ?
View SolutionTwo parallel long wire carry currents i1 and i2 with i1>i2 . When the currents are in the same direction , the magnetic field midway between the wires is 10μT . When the direction of i2 is reversed, it becomes 40μT . The ratio i1/i2 is
View Solution
