Two partical AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
π2
tan−1(45)
tan−1(34))
None of these
The correct Answer is:B
Representing a quantity with phase (ωt) along X-axis any quantity with a phase (ωt+ϕ) can be represented by a vector making an angle ϕ with a phase (ωt−ϕ) can be represented by a vector making an angle ϕ with x- axis in the clokwise sense
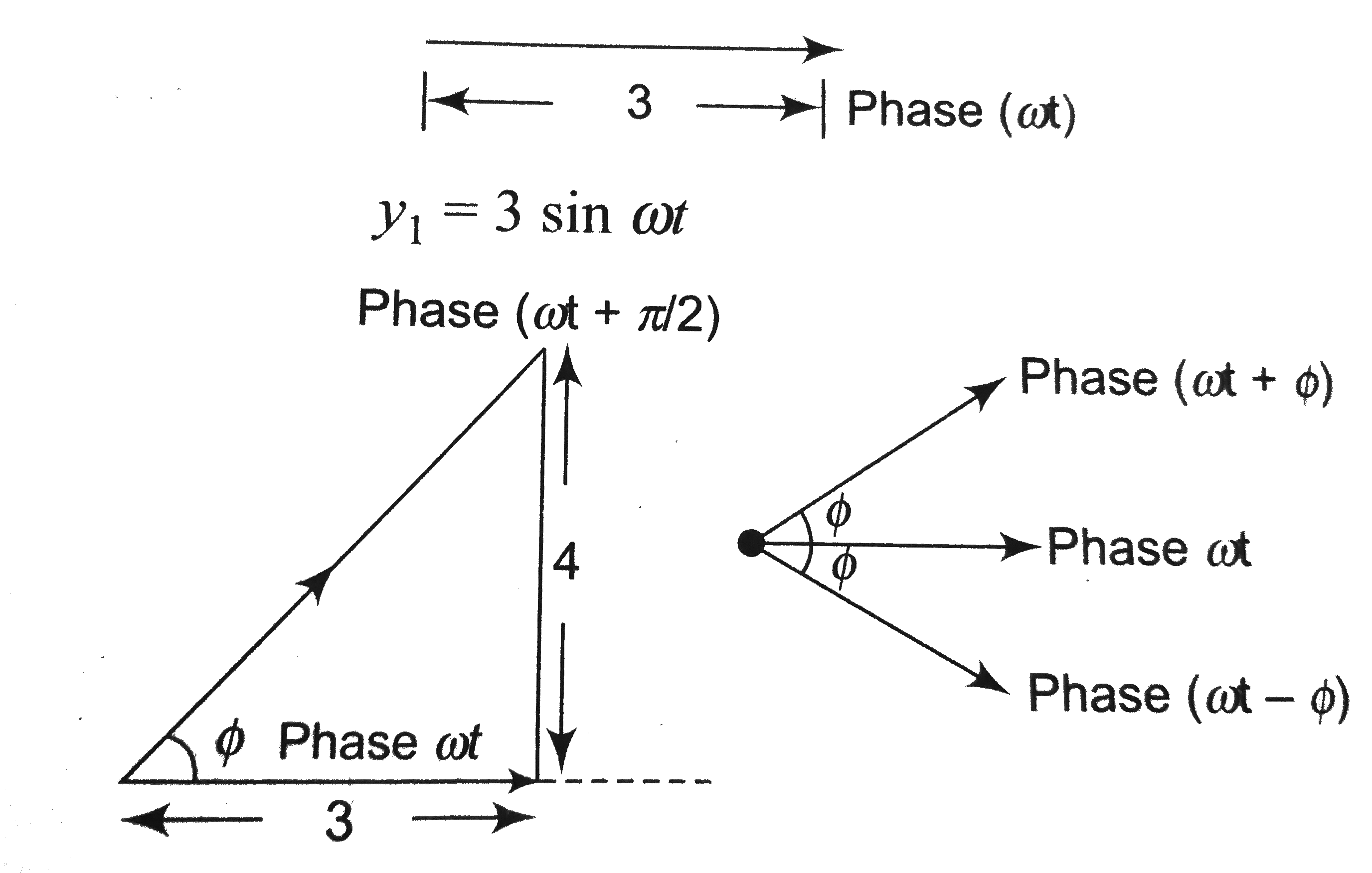
Phase difference ϕ=tan−1(45)
Altmetively given y1=3sinωt....(1)
And y2=4sin(ωt+π2)+3sinωt
=4cosωt+3sinωt=5[45cosωt+35sinωt]
=5[sinϕcosωt+cosωtsinωt]
=5sin(ωt+ϕ)

cosϕ=35sinϕ=45andtanϕ=45
From (i) and (ii) the result follows
Similar Questions
Two simple harmonic motions are represented as y1=10sinω and y2=5sinwt+5cosωt
The ration of the amplitudes of y1 and y2 is
View SolutionTwo simple harmonic motions are represented by y1=10sinωt and y2=15cosωt. The phase difference between them is
View SolutionWhat is the minimum phase difference between two simple harmonic oscillations given by y_(1)=(1)/(2) "sin" omega t+(sqrt(3))/(2) "cos" omega t y_(2)= "sin" omega t+ "cos" omega t ?
View Solutiony_(1) = 4 sin (omega t + kx), y_(2) =-4 cos(omega t + kx) , the phase difference is
View SolutionTwo waves are represented by
y1=a1cos(ωt−kx) and
y2=a2sin(ωt−kx+π/3)
Then the phase difference between them is-
View Solutiony1=asinωt और y2=bcosωt द्वारा निरूपित दो तरंगों में कलान्तर है :
View Solutionदो समीकरणें y1=Asinωt तथा y2=A2sinωt+A2cosωt सरल आवर्त गतियों को प्रदर्शित करती है। इस गतियों के आयामों का अनुपात होगा।
View Solutiony1=4sinωt तथा y2=3sin(ωt+π2) तरंगो के अध्यारोपण से बनने वाली तरंग का परिणामी आयाम होगा
View Solution

