Two particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
Method 1 : Foe bullet A. Let t be the time taken by bullet A to reach P
Vertical motion : uy=0,S=ut+12at2,Sy=−(10−y)
ay=−10ms−2⇒10−y=5t2 …(i)
Horizontal motion : x=5√3t …(ii)
For bullet B. Let (t+l) be the time taken by bullet B to reach P.
Vertical motion : ↑⏐⏐+uy=+5√3sin60∘=+7.5ms−1
S=ut+12at2,ay=−10ms−2
y−10=7.5(t+t')−5(t+t')2 ...(iii)
Horizontal motion : x=(5√3cos60∘)(t+t')
⇒5√3t+5√3t'=2x ...(iv)
Substituting the value of x from (ii) in (iv), we get
5√3t+5√3t'=10√3)t⇒t=t'
(a) Putting t=t' in (iii),
y−10=15t−20t2 ...(v)
Adding (i) and (v), 0=15t−15t2⇒t=1s
So time interval between the firings is t'=1s
(b) Putting t−1 in (ii), we get x=s√3m.
Putting t=1 in (i), we get y=5.
Therefore, the coordinates of point
Pare(5(√3,5)) in meters.
Method 2 : We take the point of firing as origin and x−andy - axis as shown in (Fig. 5.174). Equation of trajectory of the projectile is
y=xtanθ−gx22v2icos2θ
For gun 1,θ=60∘. Therefore,
y=xtan60∘−gx22v2icos260∘=x√3−2gx2v2i
For gun 2, θ=0∘. Therefore,
y=−gx22v2i
Two shots collide at point P. Therefore, their coordinates must be same.
−gx22v2i=x√3−2gx22v2i
x√3=2gx2v2i−gx22v2i=3gx22v2i
x=0 and x=2v2i√3g=2(5√3)2√3(10)=5√3
y=−gx22v2i=−10(5√3)22(5√3)2=−5m
If the origin is assigned at ground, the coordinates of point P will be (5√3)m,5m).
Now we consider the x - component of displacement for both the shots.
Gun 1 : x=5√3m=vit(5√3ms−1)t
or t1=1s
Gun 2 : x=5√3m=vicos60∘t2=5√32t2
or t2=2s
Time interval between two shots, Δt=t2−t1=1s.
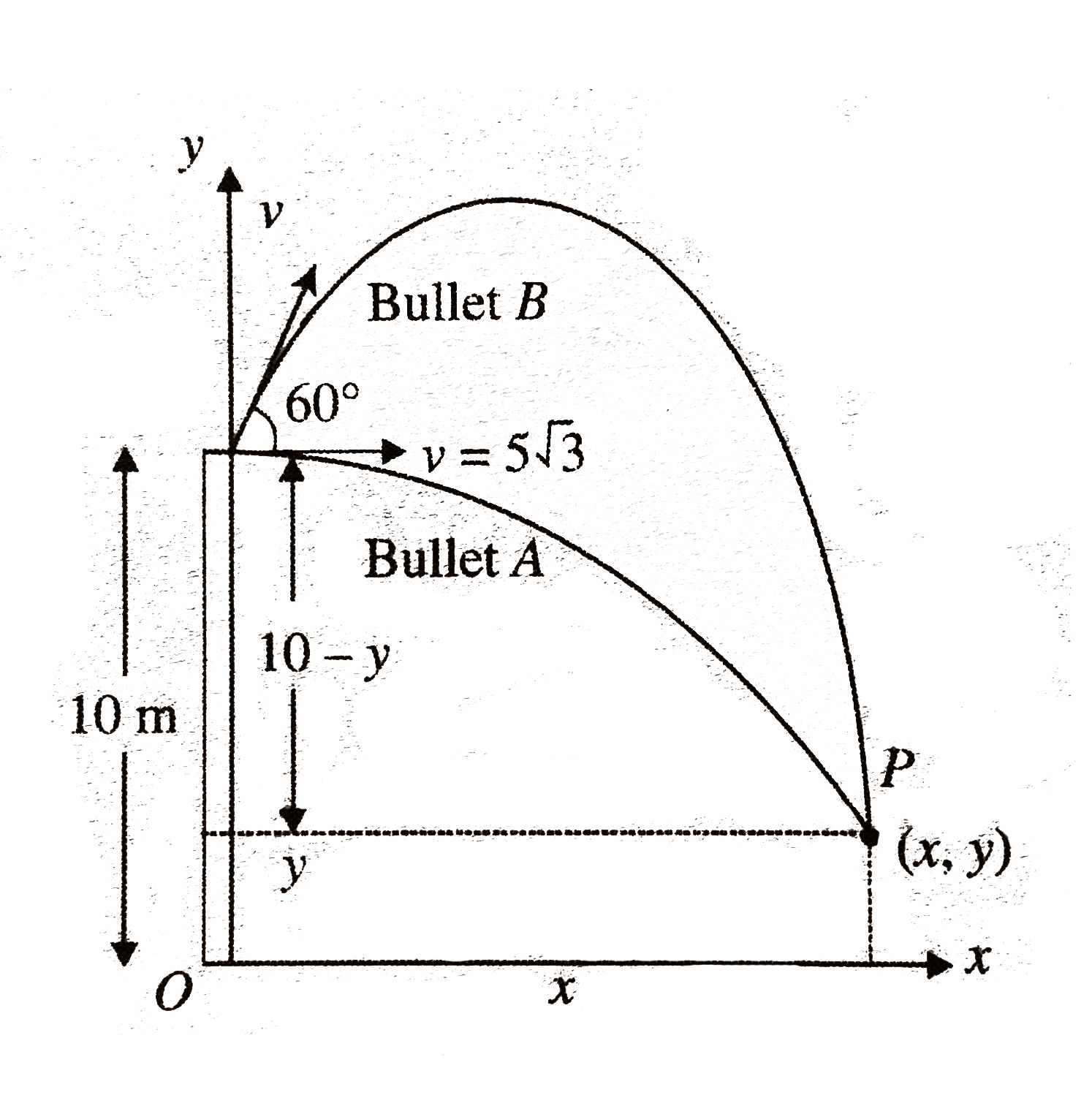 ,
, .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
24 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Two projectiles A and B are projected with same speed at an angle 30∘ and 60∘ to the horizontal, then which of the following is not valid where T is total time of flight, H is max height and R is horizontal range.
View SolutionTwo projectiles of same mass and with same velocity are thrown at an angle 60∘ and 30∘ with the horizontal, then which quantity will remain same:-
View SolutionTwo particles are projected with same initial velocity one makes angle θ with horizontal while other makes an angle θ with vertical. If their common range is R then product of their time of flight is directly proportional to :
View SolutionTwo bodies of same mass are projected with the same velocity at an angle 30∘ and 60∘ respectively.The ration of their horizontal ranges will be
View SolutionTwo particles are projected with same velocity but at angles of projection 25° and 65° with horizontal. The ratio of their horizontal ranges is
View SolutionTwo particles are projected with same velocity but at angles of projection 35° and 55°. Then their horizontal ranges are in the ratio of
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)

View SolutionFour projectiles are projected with the same speed at angles 20∘,35∘,60∘and75∘
with the horizontal. The range will be the maximum for the projectile whose angle of projection is
View SolutionA particle is projected from ground with an initial velocity 20m/sec making an angle 60∘ with horizontal . If R1 and R2 are radius of curvatures of the particle at point of projection and highest point respectively, then find the value of R1R2.
View Solution

