two particle of medium disturbed by the wave propagation are at x1=0andx2=1cm. The respective displacement (in cm) of the particles can be given by the equation:
y1=2sin3πt,y2sin(3πt−π/8) the wave velocity is
16cm/s
24cm/s
12cm/s
8cm/s
The correct Answer is:b
To find the wave velocity given the displacements of two particles in a medium, we can follow these steps:
Step 1: Identify the equations of the displacements
The displacements of the particles at positions x1=0 cm and x2=1 cm are given by:
- y1=2sin(3πt)
- y2=sin(3πt−π8)
Step 2: Compare with the standard wave equation
The standard equation for a traveling wave can be expressed as:
y=asin(ωt−kx)
where:
- a is the amplitude,
- ω is the angular frequency,
- k is the wave number.
Step 3: Determine the angular frequency ω
From the equation for y1:
y1=2sin(3πt)
we can see that:
- ω=3π
Step 4: Determine the wave number k
From the equation for y2:
y2=sin(3πt−π8)
we can rewrite it in the form y=asin(ωt−kx) by noting that the term −π8 corresponds to the spatial part. Since y2 is given at x2=1 cm, we can express it as:
y2=sin(3πt−k⋅1)
This implies:
k=3π−π8
Step 5: Calculate the wave number k
To find k, we need to express it in terms of the wave number:
From the equation:
k=ωv
We can also find k directly from the wave number relationship. However, since we already have ω, we can find k from the given displacement equations.
Step 6: Calculate the wave velocity v
The wave velocity v is given by the formula:
v=ωk
Substituting the values we found:
- ω=3π
- k=π8
Thus:
v=3ππ8=3π⋅8π=24cm/s
Conclusion
The wave velocity is 24cm/s.
The displacements of the particles at positions x1=0 cm and x2=1 cm are given by:
- y1=2sin(3πt)
- y2=sin(3πt−π8)
The standard equation for a traveling wave can be expressed as:
y=asin(ωt−kx)
where:
- a is the amplitude,
- ω is the angular frequency,
- k is the wave number.
From the equation for y1:
y1=2sin(3πt)
we can see that:
- ω=3π
From the equation for y2:
y2=sin(3πt−π8)
we can rewrite it in the form y=asin(ωt−kx) by noting that the term −π8 corresponds to the spatial part. Since y2 is given at x2=1 cm, we can express it as:
y2=sin(3πt−k⋅1)
This implies:
k=3π−π8
To find k, we need to express it in terms of the wave number:
From the equation:
k=ωv
We can also find k directly from the wave number relationship. However, since we already have ω, we can find k from the given displacement equations.
The wave velocity v is given by the formula:
v=ωk
- ω=3π
- k=π8
v=3ππ8=3π⋅8π=24cm/s
The wave velocity is 24cm/s.
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Single Correct Answer
Explore 1 Video
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Multiple Correct
Explore 25 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Subjective
Explore 16 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICS ENGLISHChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The figure shows three progressive waves A, B and c. wahat canbe concluded from the figure that with respect to wave A?
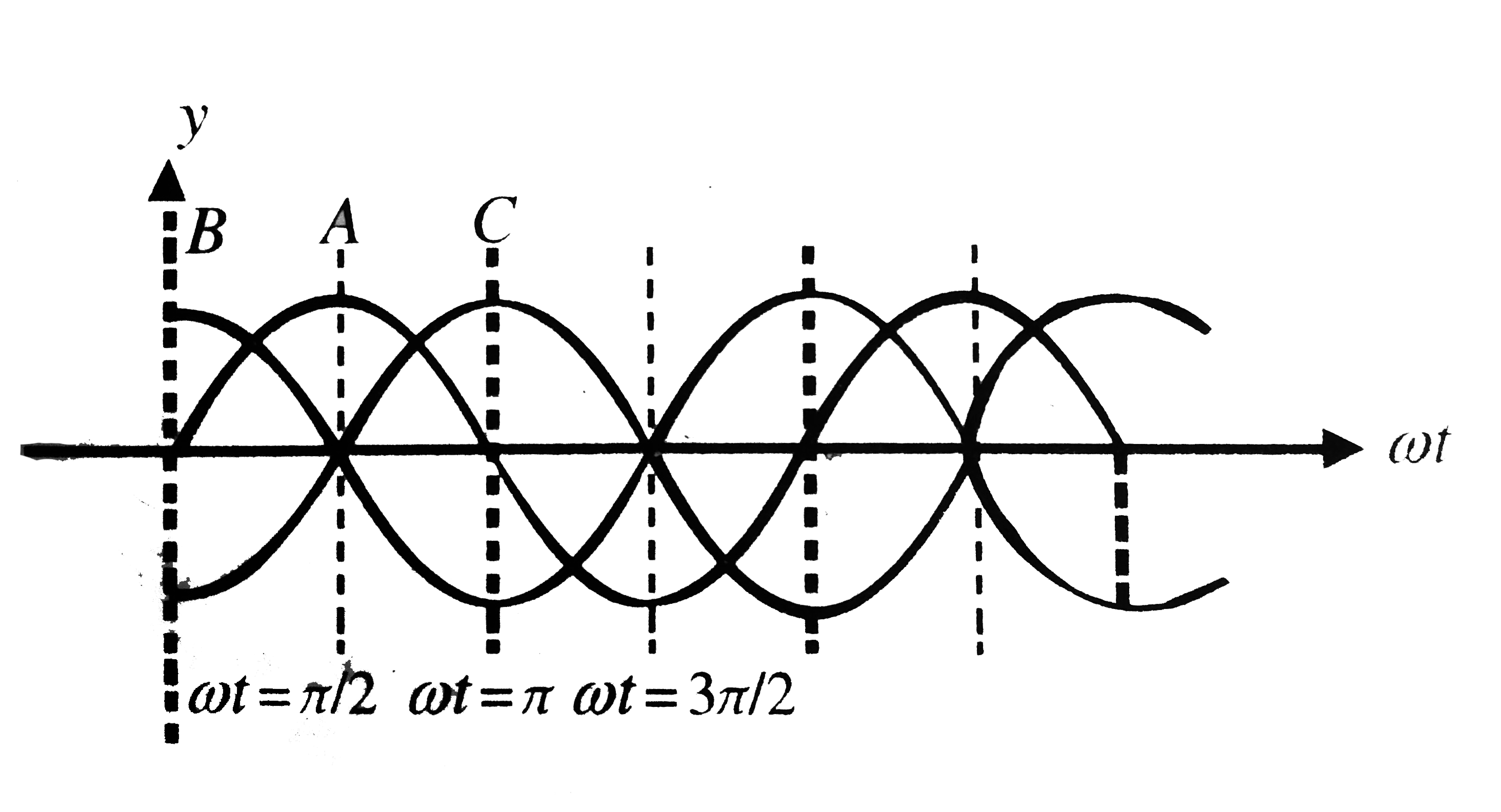
View SolutionA wave equation which gives the displacement along the y-direction is given by y=10−4sin(60t+2x) where xandy are in meters and t is time in seconds. This represents a wave
View SolutionA 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionIf the point x_(1)+t(x_(2)-x_(1)),y_(1)+t(y_(2)-y_(1)) divides the join of (x_(1),y_(1)) and (x_(2),y_(2)) internally then locus of t is
View Solutiontwo particle of medium disturbed by the wave propagation are at x1=0andx2=1cm. The respective displacement (in cm) of the particles can be given by the equation:
y1=2sin3πt,y2sin(3πt−π/8) the wave velocity is
View SolutionLet a disturbance y be propagated as a plane wave along the x-axis. The wave profile at the instants t=t_(1) and t=t_(2) are represent respectively as: y_(1)=f(x_(1)-vt_(1)) and y_(2)=f(x_(2)-vt_(2)). The wave is propagating withoute change of shape.
View SolutionTwo particles of a medium disturbed by the wave propagtion are at x_(1)=0 and x_(2)=1 cm The wave is propagating in positive x-direction The displacement of the particles is given by the equation: y_(1)=(2sin3pit) cm and y_(2)=2sin(3pit-pi//8) cm (t is in seconds)
View SolutionWave equations of two particles are given by y_(1)=a sin (omega t -kx), y_(2)=a sin (kx + omega t) , then
View SolutionEquations of a stationery and a travelling waves are y_(1)=a sin kx cos omegat and y_(2)=a sin (omegat-kx) The phase differences between two between x_(1)=(pi)/(3k) and x_(2)=(3pi)/(2k) are phi_(1) and phi_(2) respectvely for the two waves. The ratio (phi_(1))/(phi_(2)) is
View SolutionTwo particles of of a medium disturbed by the wave propagation are at x1=0 and x2=1cm. The wave is propagating in positive x-direction. The displacement of the particles is given by the equation :
y1=(2sin3πt)cm and y2=2sin(3πt−π/8)cm (t is in second
View SolutionIf two particles performing SHM, are given by,
x1=10sin[3πt+(π/4)]and
x2=5[sin3πt+√3cos3πt]
then the ratio of their amplitudes is
View Solutionदो तरंगों के विस्थापन का समीकरण निम्न है :
y1=10sin[3πt+π/3] व y2=5[sin3πt+cos3πt] इनके आयामों का अनुपात कितना होगा?
View SolutionA stationary wave is formed by superposition of two waves given by
64.88 y1=0.02sin(3πt−x)andy2=0.02sin(3πt+x)
where x, y are in metres and t is in seconds. Determine the displacement of a particle situated at a distance of x = 0.5 m.
View Solution
