_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
v=√GmR
v=√Gm2R
v=12√GmR
v=√4GmR
The correct Answer is:C
As gravitational force provides the centripetal force to the satellite to revolve around the earth
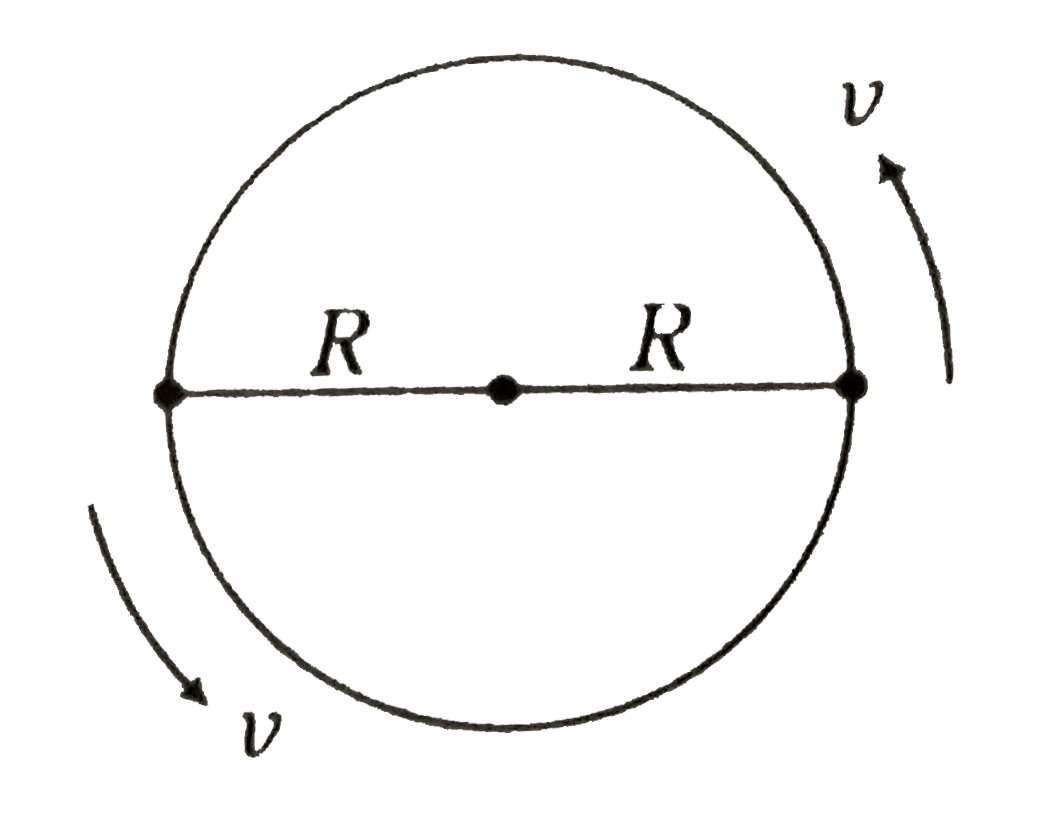
G.m.m4R2=mv2(R)⇒v=12√GmR
Similar Questions
Two particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFor particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2RTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
A13√GmRB12√GmRC12√RGmD√GmRTwo particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
A√Gm4RB√Gm3RC√Gm2RD√GmR
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.

View SolutionTwo particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
View Solution
