Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
To solve the problem, we need to find the displacement of a particle at time t=2 seconds, given that its velocity varies with displacement as v=√4+4s m/s and that the initial displacement at t=0 is s=0.
1. Square the Velocity Equation:
v=√4+4s
Squaring both sides gives:
v2=4+4s
2. Identify Initial Conditions:
At t=0, the displacement s=0. Thus, we can find the initial velocity v when s=0:
v2=4+4(0)=4⟹v=√4=2m/s
So, the initial velocity u=2m/s.
3. Determine Acceleration:
From the equation v2=u2+2as, we can compare:
v2=4+4sandu2=4
This implies:
2a=4⟹a=2m/s2
4. Use the Kinematic Equation:
We can now use the kinematic equation to find the displacement s at t=2 seconds:
s=ut+12at2
Substituting the known values:
u=2m/s,t=2s,a=2m/s2
s=(2)(2)+12(2)(22)
s=4+12(2)(4)=4+4=8m
5. Final Answer:
The displacement of the particle at t=2 seconds is:
s=8meters
v=√4+4s
Squaring both sides gives:
v2=4+4s
At t=0, the displacement s=0. Thus, we can find the initial velocity v when s=0:
v2=4+4(0)=4⟹v=√4=2m/s
So, the initial velocity u=2m/s.
From the equation v2=u2+2as, we can compare:
v2=4+4sandu2=4
This implies:
2a=4⟹a=2m/s2
We can now use the kinematic equation to find the displacement s at t=2 seconds:
s=ut+12at2
Substituting the known values:
u=2m/s,t=2s,a=2m/s2
s=(2)(2)+12(2)(22)
s=4+12(2)(4)=4+4=8m
The displacement of the particle at t=2 seconds is:
s=8meters
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.1
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.2
3 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 7
1 Video
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
"A lift is ascending with decreasing speed". What are the directions of velocity and acceleration of the lift at the given instant.
View SolutionVelocity and acceleration of a particle are v=(2ˆi−4ˆj)ms and a=(−2ˆi+4ˆj)ms2 Which type of motion is this?
View SolutionA particle is moving along x-axis. At time t=0, Its x-coordinate is x=−4m. Its velocity-time equation is v=8−2t where, v is in m//s and t in seconds.
(a) At how many times, particle is at a distance of 8m from the origin?
(b) Find those times.
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionA stone is dropped from a certain height which can reach the ground in 5s. It is stopped after 3s of its fall and then it is again released. The total time taken by the stone to reach the ground will be .
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
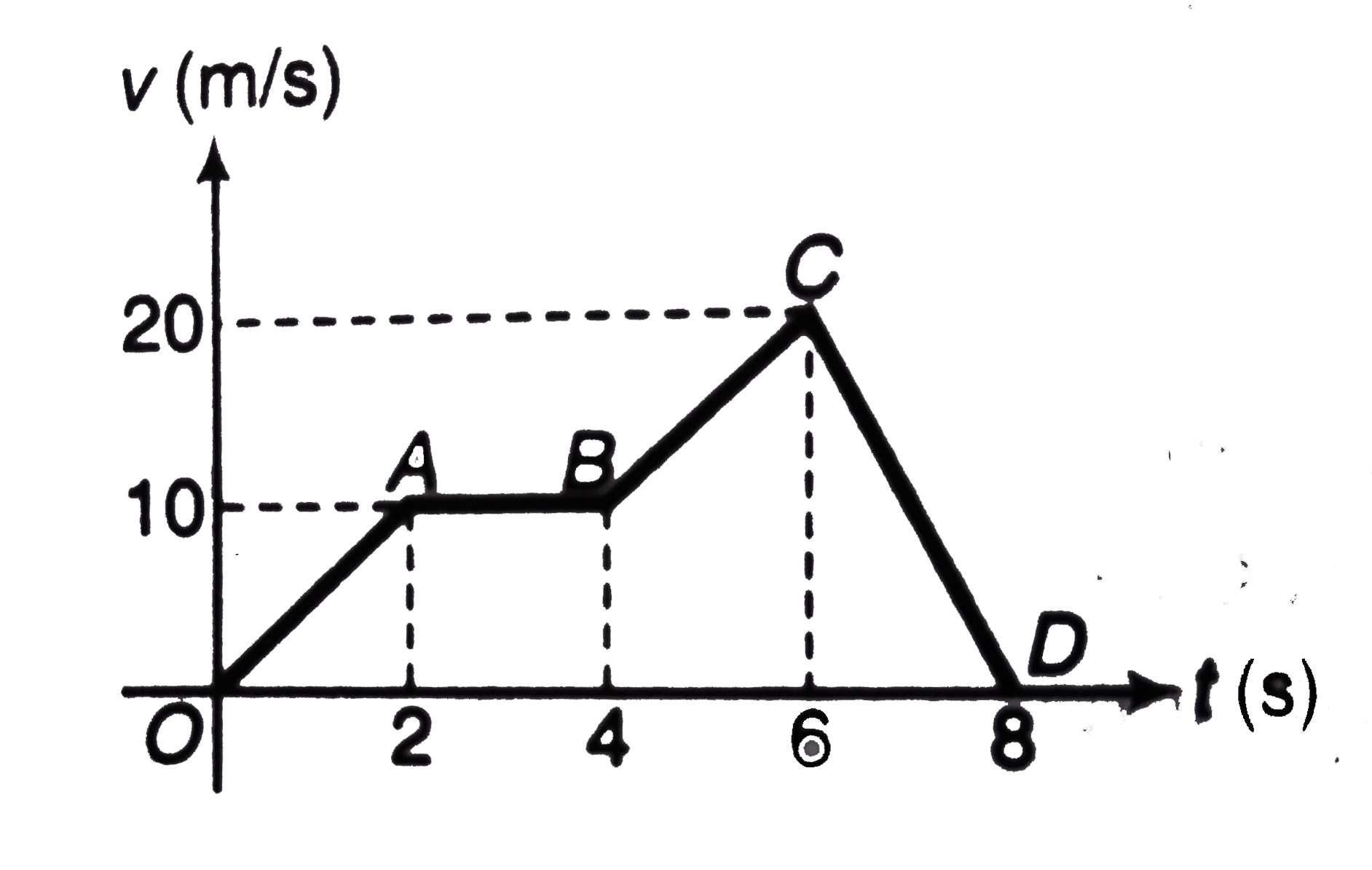
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
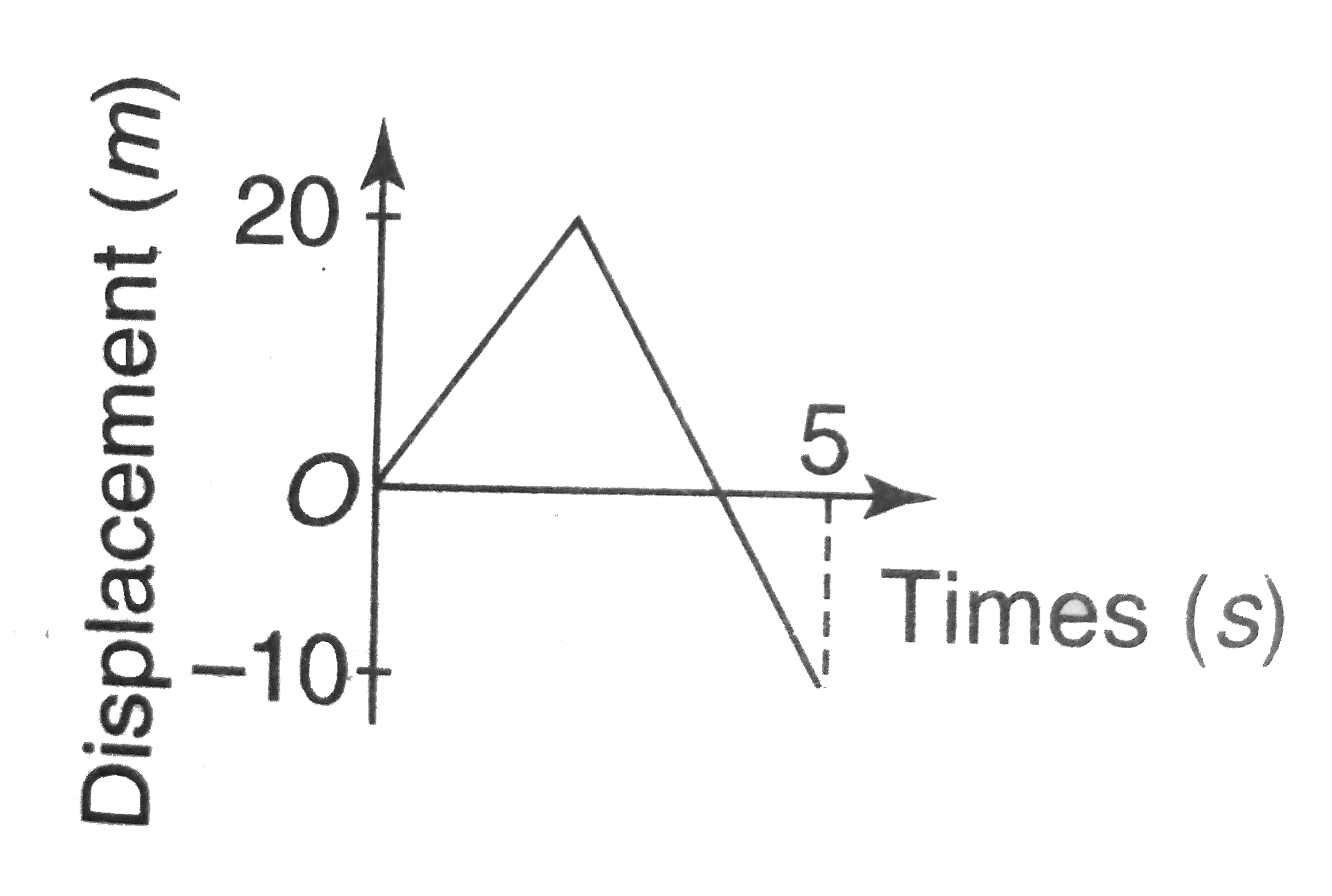
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View SolutionFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=√4+4xm/s where x is displacement. Displacement of particle at time t = 0 is x = 0. Find displacement (in m) of particle in 2 sec.
View SolutionIf displacements of a particle varies with time t as s = 1/t^(2) , then.
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
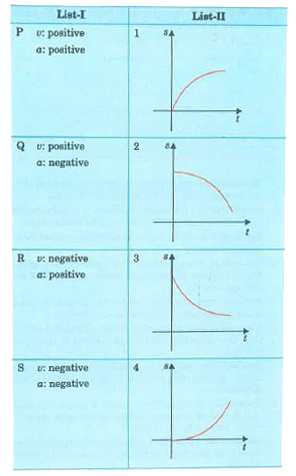
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View Solution

