Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
50
51
48
51.5
The correct Answer is:A
To solve the problem, we will use Bernoulli's principle and the equation of continuity. Here are the steps to find v2, the square of the velocity of water coming out of the hole.
Step 1: Understand the given data
- Height of water in the container, H=3m=300cm
- Height of the hole from the bottom, h=52.5cm
- Area of the hole, a
- Cross-sectional area of the container, A
- Given ratio aA=0.1
Step 2: Calculate the effective height of water above the hole
The effective height h′ of water above the hole is calculated as:
h′=H−h=300cm−52.5cm=247.5cm=2.475m
Step 3: Apply Bernoulli's equation
According to Torricelli's law, the velocity v of efflux from the hole can be given by:
v=√2gh′
where g is the acceleration due to gravity, approximately 10m/s2.
Step 4: Substitute the values into the equation
Substituting g=10m/s2 and h′=2.475m:
v=√2⋅10⋅2.475
Step 5: Calculate v2
Calculating v2:
v2=2⋅10⋅2.475=49.5m2/s2
Step 6: Adjust for the area ratio
Since the area of the hole is much smaller than the cross-sectional area of the container, we need to consider the effect of the area ratio. The formula for the velocity considering the area ratio is:
v2=2gh′1−aA2
Substituting aA=0.1:
v2=49.5(1−0.1)2=49.5(0.9)2=49.50.81≈61.11m2/s2
Final Result
Thus, the square of the velocity of water coming out of the hole is approximately:
v2≈61.11m2/s2
- Height of water in the container, H=3m=300cm
- Height of the hole from the bottom, h=52.5cm
- Area of the hole, a
- Cross-sectional area of the container, A
- Given ratio aA=0.1
The effective height h′ of water above the hole is calculated as:
h′=H−h=300cm−52.5cm=247.5cm=2.475m
According to Torricelli's law, the velocity v of efflux from the hole can be given by:
v=√2gh′
where g is the acceleration due to gravity, approximately 10m/s2.
Substituting g=10m/s2 and h′=2.475m:
v=√2⋅10⋅2.475
Calculating v2:
v2=2⋅10⋅2.475=49.5m2/s2
Since the area of the hole is much smaller than the cross-sectional area of the container, we need to consider the effect of the area ratio. The formula for the velocity considering the area ratio is:
v2=2gh′1−aA2
Substituting aA=0.1:
v2=49.5(1−0.1)2=49.5(0.9)2=49.50.81≈61.11m2/s2
Thus, the square of the velocity of water coming out of the hole is approximately:
v2≈61.11m2/s2
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:AR_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:MCQ_TYPE
Explore 3 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:True/False
Explore 1 Video
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
STATEMENT-1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
STATEMENT-2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
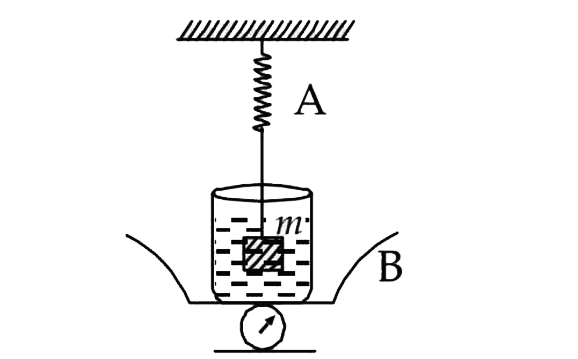
View SolutionThe spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass in inside the liquid in the beaker as shown in the figure. In this situation:
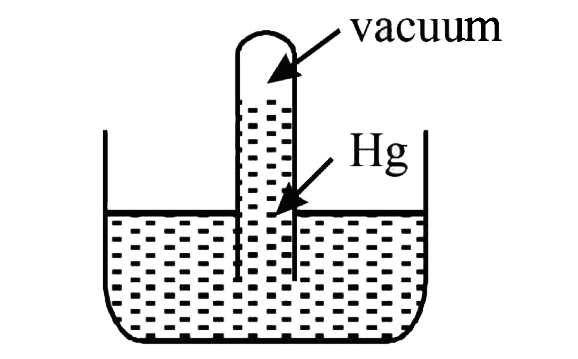
View SolutionA barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionGravitational acceleration on the surface of a planet is √611g. where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is 23 times that of the earth. If the escape speed on the surface of the earht is taken to be 11kms−1 the escape speed on the surface of the planet in kms−1 will be
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a//A=0.1 then v^2 is (where v is the velocity of water coming out of the hole)
View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height 'h'. The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is 'a' and that of the top surface is 'A') :
View Solutionएक बेलनाकार बर्तन में 3 मीटर की ऊँचाई तक जल भरा है । बर्तन की दीवार में, तली से 52.5 सेमी की ऊँचाई पर परिच्छेद - क्षेत्रफल a का एक छिद्र बना है । बर्तन का परिच्छेद - क्षेत्रफल A है । यदि aA=0.1, तो छिद्र से निकलने वाले जल की चाल का वर्ग है (g=10 मीटर/सेकण्ड2) :
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA cylinder contains a liquid upto a height 2.5 m . If now a small hole is made at bottom . Liquid comes out with a velocity
View Solutiona_(1) A reservoir filled with cross-sectional area is waterlogged to a height of h. At the bottom of the reservoir a_(2) There is a hole in the area. a_(1)=3a_(2) The initial velocity of water coming out through the hole is
View SolutionOil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
View SolutionA cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g= 10 m//s^(2) )
View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View Solution
