We know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
A charge particle of mass 10 mg and charge 2.5μC is released from rest at x=2m. Find its velocity when it crosses origin.
0.5ms−1
1ms−1
2ms−1
4ms−1
The correct Answer is:C
E=−dVdx=−4x
F=qE=2.5×10−6(−4x)=−10−5x
W=0∫2Fdx=−10−50∫2xdx
12mv2=10−5[x22]20 or V=2ms−1
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Interger Answer type
Explore 20 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Fill in the blanks
Explore 10 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Assertion and Reason Type
Explore 8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 11 Videos
Similar Questions
We know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionThe variation of potential with distance R from a fixed point is shown in figure. The electric field at R = 5 m is -
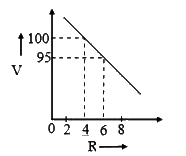
View SolutionThe variation of potential with distance r from a fixed point is shown in fig. The electric field at r = 5cm, is :

View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
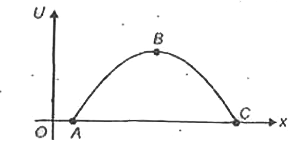
The body is in equilibrium state at
View SolutionThe electrostatic potential V at any point (x, y, z) in space is given by V=4x2
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point is
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point is
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point is
View SolutionAn α particle is placed in an electric field at a point having electric potential 5V. Find its potential energy ?
View SolutionThe electric potential at any point x,yandz in metres is given by V=3x2. The electric field at a point (2,0,1) is
View Solution
