We would like to perpare a scale whose length does not change with temperature. It is proposed to prepare a unit scale f this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length (both components) would change in such a way that differnece between theri lenght rermain constant. If αiron=1.2×10−5/Kandαbrass=1.8×10−5/K, what should we take as lenght of each strip ?
To solve the problem of determining the lengths of the brass and iron strips in a bimetallic strip that maintains a constant length of 10 cm, we can follow these steps:
1. Define Variables:
Let Li be the length of the iron strip and Lb be the length of the brass strip. According to the problem, the difference in their lengths should remain constant at 10 cm:
Li−Lb=10 cm
2. Final Lengths After Temperature Change:
When the temperature changes, the lengths of the strips will change according to their coefficients of linear expansion. The final lengths can be expressed as:
Li,f=Li(1+αiΔT)
Lb,f=Lb(1−αbΔT)
where αi=1.2×10−5K−1 (iron) and αb=1.8×10−5K−1 (brass).
3. Set Up the Equation for Final Lengths:
Since the difference in lengths must remain constant, we can set up the equation:
Li,f−Lb,f=Li−Lb
Substituting the expressions for Li,f and Lb,f:
Li(1+αiΔT)−Lb(1−αbΔT)=10
4. Rearranging the Equation:
Rearranging gives:
Li+LiαiΔT−Lb+LbαbΔT=10
Simplifying further:
LiαiΔT+LbαbΔT=10−(Li−Lb)
Since Li−Lb=10:
LiαiΔT+LbαbΔT=0
5. Factor Out ΔT:
Since ΔT≠0, we can factor it out:
Liαi=Lbαb
6. Express Li in Terms of Lb:
Rearranging gives:
LiLb=αbαi
Substituting the values of αb and αi:
LiLb=1.8×10−51.2×10−5=32
Thus, we can express Li as:
Li=32Lb
7. Substitute Back to Find Lengths:
Now substituting Li back into the equation Li−Lb=10:
32Lb−Lb=10
This simplifies to:
12Lb=10⟹Lb=20 cm
8. Calculate Li:
Now substituting Lb back to find Li:
Li=32×20=30 cm
Final Answer:
- Length of the iron strip, Li=30 cm
- Length of the brass strip, Lb=20 cm
Let Li be the length of the iron strip and Lb be the length of the brass strip. According to the problem, the difference in their lengths should remain constant at 10 cm:
Li−Lb=10 cm
When the temperature changes, the lengths of the strips will change according to their coefficients of linear expansion. The final lengths can be expressed as:
Li,f=Li(1+αiΔT)
Lb,f=Lb(1−αbΔT)
where αi=1.2×10−5K−1 (iron) and αb=1.8×10−5K−1 (brass).
Since the difference in lengths must remain constant, we can set up the equation:
Li,f−Lb,f=Li−Lb
Substituting the expressions for Li,f and Lb,f:
Li(1+αiΔT)−Lb(1−αbΔT)=10
Rearranging gives:
Li+LiαiΔT−Lb+LbαbΔT=10
Simplifying further:
LiαiΔT+LbαbΔT=10−(Li−Lb)
Since Li−Lb=10:
LiαiΔT+LbαbΔT=0
Since ΔT≠0, we can factor it out:
Liαi=Lbαb
Rearranging gives:
LiLb=αbαi
Substituting the values of αb and αi:
LiLb=1.8×10−51.2×10−5=32
Thus, we can express Li as:
Li=32Lb
Now substituting Li back into the equation Li−Lb=10:
32Lb−Lb=10
This simplifies to:
12Lb=10⟹Lb=20 cm
Now substituting Lb back to find Li:
Li=32×20=30 cm
- Length of the iron strip, Li=30 cm
- Length of the brass strip, Lb=20 cm
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT EXEMPLAR ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Very short Answer type Questions
Explore 15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
- THERMODYNAMICS Book:NCERT EXEMPLAR ENGLISHChapter:THERMODYNAMICS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
Is the bulb of a thermoeter made of diathermic or adiabatic wall ?
View SolutionFind the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
View SolutionConsider a P−V diagram in which the path followed by one mole of perfect gas in a cyclinderical container is shown in (figure)
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures T1/T2,ifV2=2V1?
(c ) Given the internal energy for one mole of gas at temperature Tis(3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2=2V1.
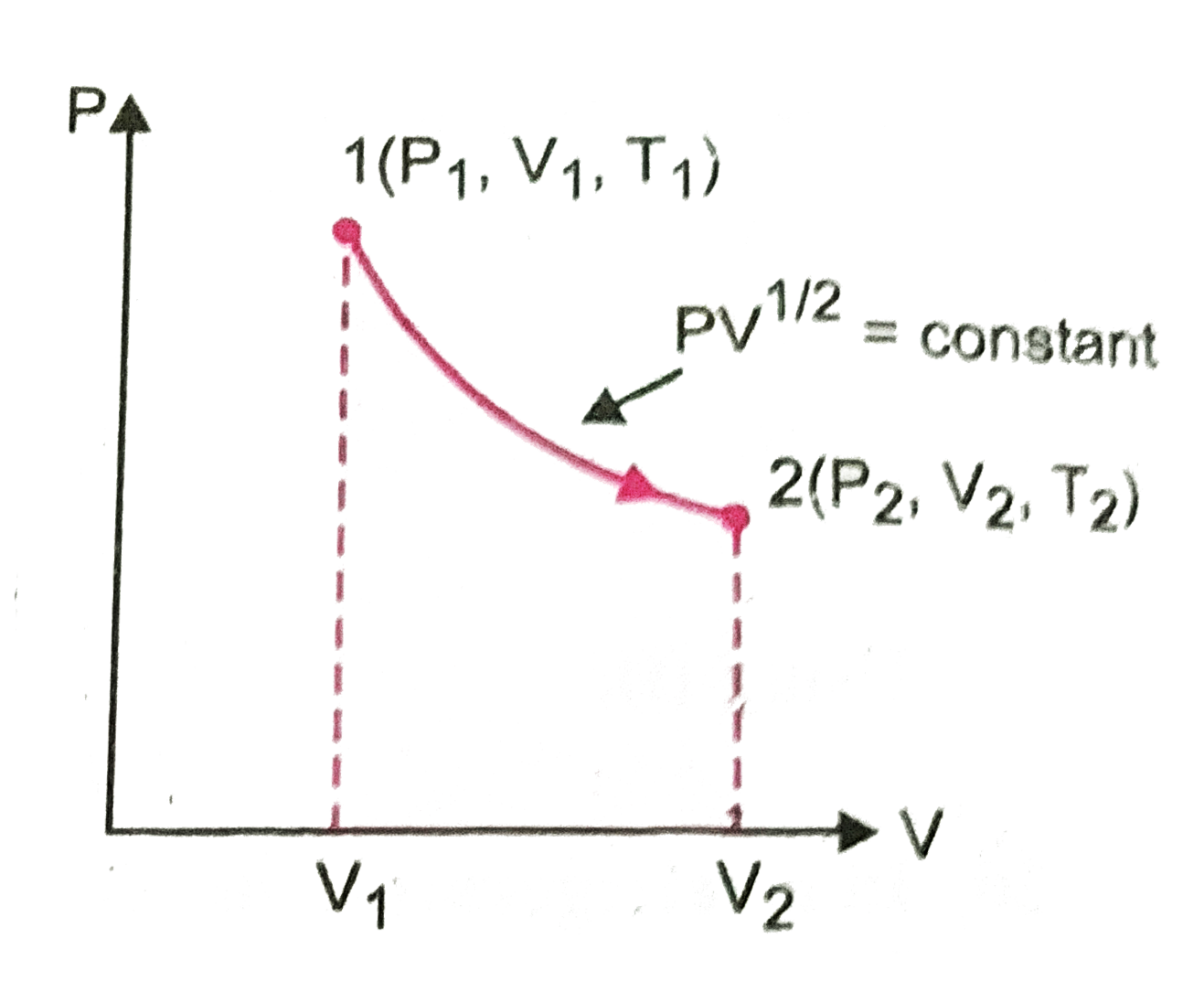
View SolutionThe length of s steel rod exceeds that of a brass rod by 5 cm. If the difference in their lengths remains same at all temperature, then the length of brass rod will be: (α for iron and brass are 12×10−6/∘C and 18×10−6/∘C, respectively)
View SolutionWe would like to perpare a scale whose length does not change with temperature. It is proposed to prepare a unit scale f this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length (both components) would change in such a way that differnece between theri lenght rermain constant. If alpha_(iron) = 1.2 xx 10^(-5)//K and alpha_(brass) = 1.8 xx 10^(-5)//K, what should we take as lenght of each strip ?
View SolutionWe would like to make a vessel whose volume does not change with temperature (take a hing from the problem aobve). We can use brass and iron (beta_(brass) = 6 xx10^(-5) // K and beta_(iron) = 3.55 xx 10^(-5)//K) ot create a volume of 100 c c. How do you think you can achieve this.
View SolutionA brass scale gives correct length at 0∘C. If the temperature by 25∘C and the length read by the scale is 10cm. Then the actual length will be
View SolutionThe length of a brass rod at 20^@C is observed to be 0.8 m when measured by an iron scale, correct at 0^@C . What will be the correct length of the rod at 0^@C ? Take, alpha_("iron") = 1.2 xx 10^(-5) ""^@C^(-1) alpha_("brass") = 1.9 xx 10^(-5) ""^@C^(-1)
View SolutionBy a steel scale, the length of a copper wire is measured to be 80.0 cm. 20^(@) C is the temperature (which is the calibration temperature of the scale) 40^(@) C will be the length of the wire measured by the scale at the temperature ( alpha_(इस्ताप) = 11 xx 10^(-6) per^(@) C And alpha_(तांबा) = 17 xx 10^(-6)"per "^(@)C )
View SolutionWe would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If alpha_("iron")=1.2xx10^(-5)//K and alpha_("brass")=1.8xx10^(-5)//K what should we take as length of each strip ?
View SolutionWe would like to make a vessel whose volume does not change with temperature . We can use brass and iron (beta_(brass) = 6 xx10^(-5) // K and beta_(iron) = 3.55 xx 10^(-5)//K) at create a volume of 100 c c. How do you think you can achieve this.
View SolutionA brass scale correctly calibrated at 15°c is employed to measure a length at a temperature of 35°C. It the scale measures a reading of 75 cm (αbrass=2×10−5/∘C)
View SolutionWhen a brass rod is put in a furnace, its length increases by 1 %. If the room temperature is 25°C and αBrass=20×10−6/∘C, the change in. the temperature is 100x∘C, where x=
View SolutionThe difference between the lengths of steel rod and a brass rod is 0.6 at all temperatures. What are their lengths at 0^@C ? (alpha_Steel = 12 xx 10^-6//^@C , (alpha_(brass)= 18 xx 10^-6//^@C )
View SolutionThe length of steel rod exceeds that of a brass rod by 5 cm. If the difference in their lengths remains same at all temperature, then the length of brass rod will be: ( alpha for iron and brass are 12xx10^(-6)//^(@)C and 18xx10^(-6)//^(@)C , respectively)
View Solution
