What is the radius of curvature of the parabola traced out by the projectile in the previous problem projected with speed v at an angle of theta with the horizontal at a point where the particle velocity makes an angle θ2 with the horizontal?
u2cos2sec3(θ2)g
u2cos2sec3(θ2)2g
2u2cos2θsec3(θ2)g
u2cos2θsec3(θ2)√3g
The correct Answer is:A
(a) We know that ac=v2r⇒r=v2ac, where r is known as radius of curvature. At the highest point, v=ucosθ,
ac=g⇒r=u2cos2θg
Similarly, find the velocity and ac at the given point and then find r.ac will be component of g perpendicular to velocity at that point (Fig. S5.93).
vcos(θ/2)=ucosθ
⇒v=ucosθsec(θ/2)
ac=gcos(θ/2)
Now find r=v2ac
h=H/2,vcosϕ=ucosθ ...(i)
v2sin2ϕ=u2sin2θ−2g(H)2...(ii)
Squaring Eq. (i) and adding in Eq. (ii), we get
v2=u2−gH where H=u2sinθ2g
ac=gcosϕ=gucosθv
Now r=v2ac.
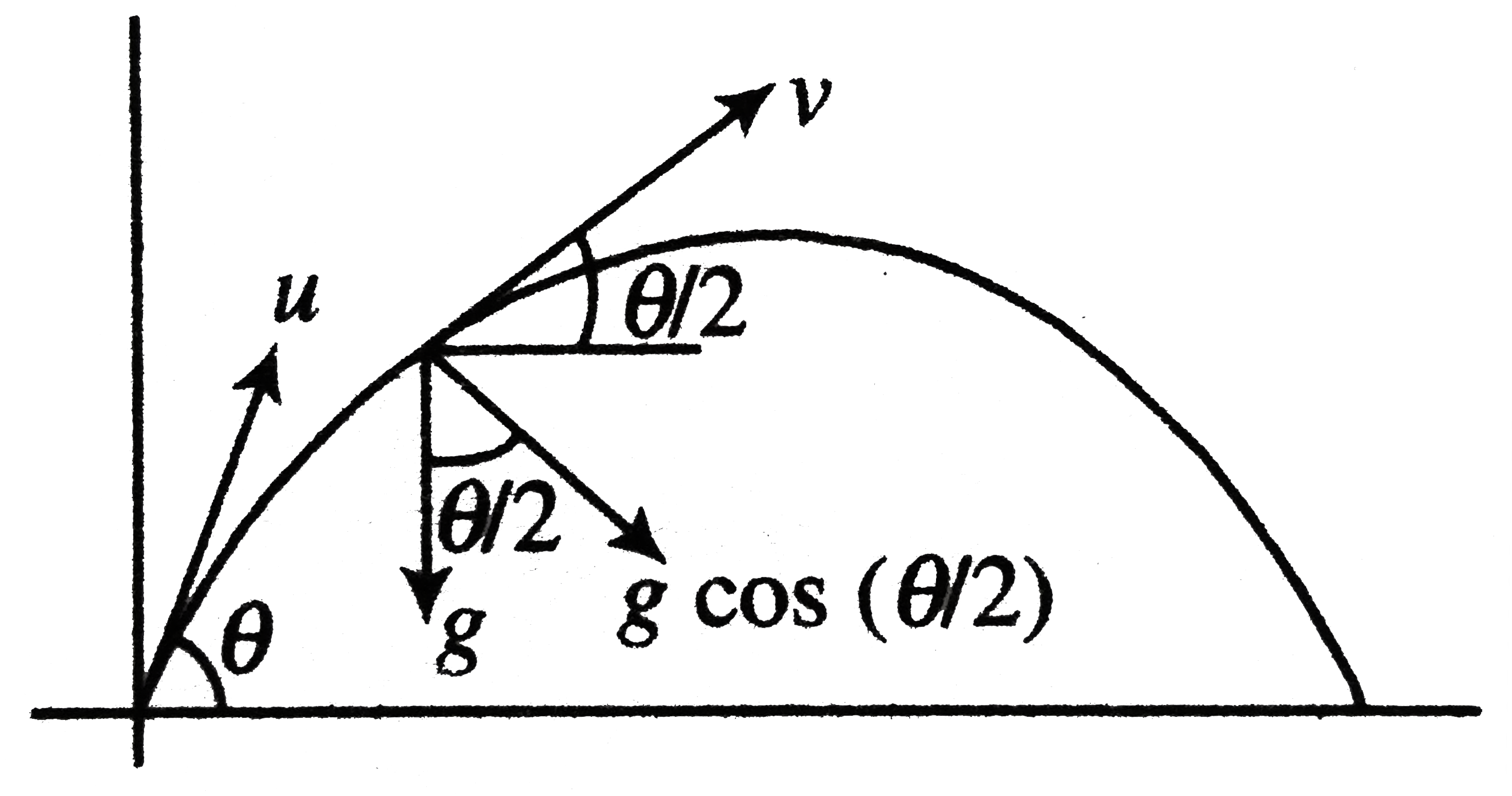 ,
,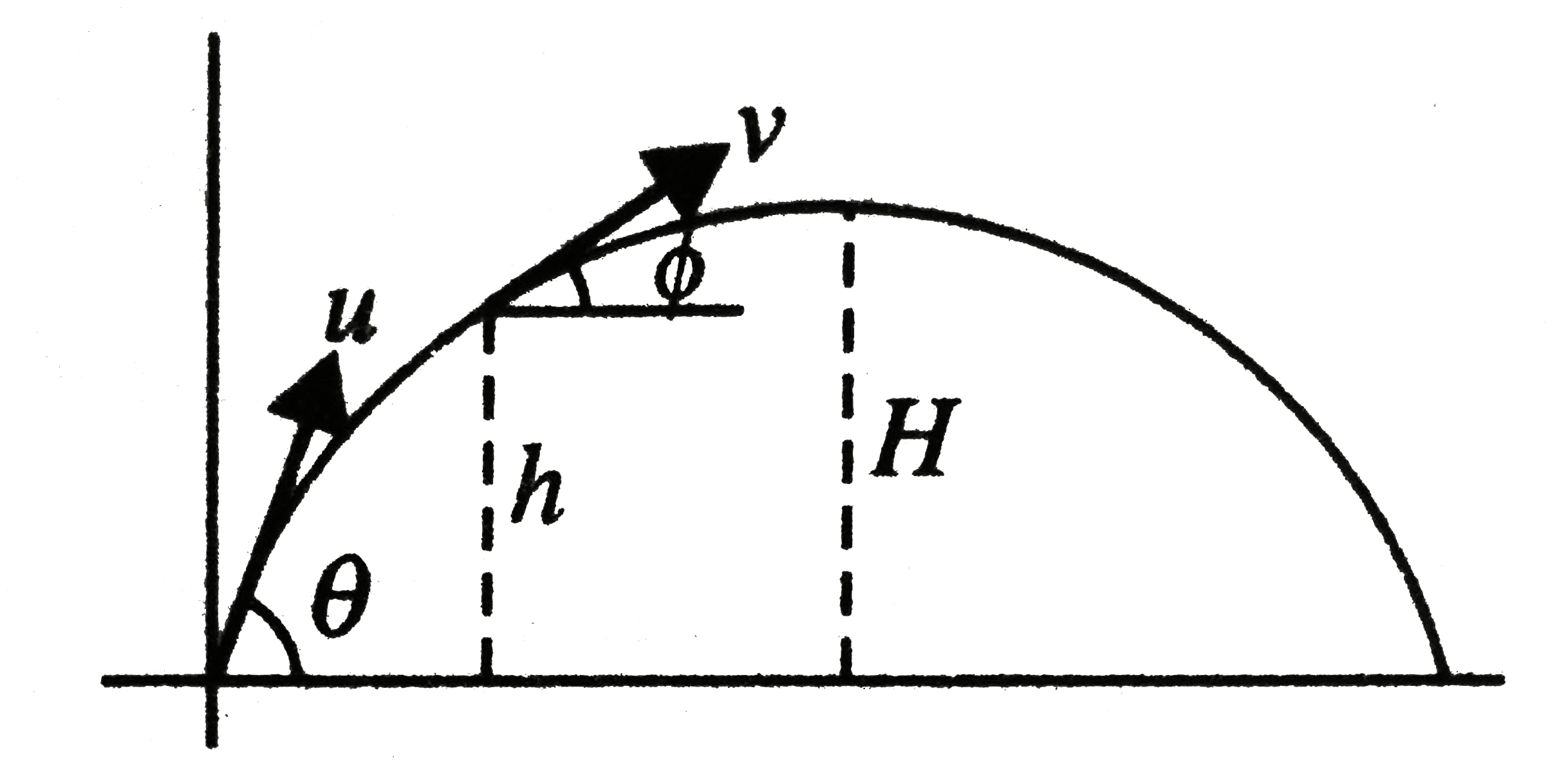 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
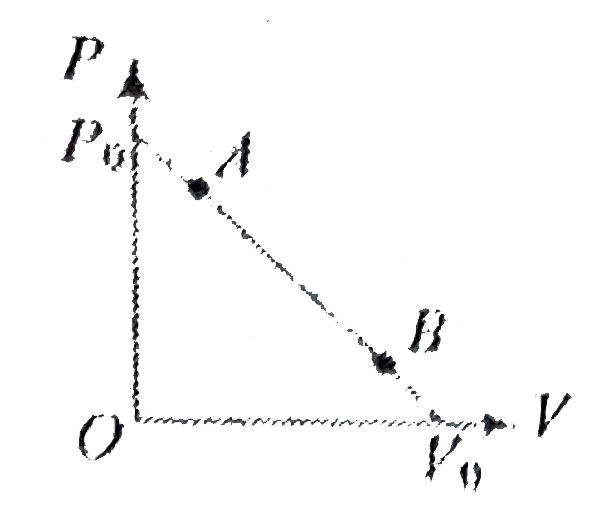
The absolute temperature T versus volume V for the given process is
View SolutionA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
View SolutionA projectile is projected with a speed u at an angle theta with the horizontal. What is the speed when its direction of motion makes an angle theta//2 with the horizontal
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile.Projected with a speed u=√30 at angle θ=60∘ with the horizontal at a point where the particle velocity makes an angle θ/2 with the horizontal ?
View SolutionA particle is projected with speed u at angle theta to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View SolutionA particle is projected from ground at an angle theta with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
View SolutionA body is projected with a speed u at a angle theta with the horizonatl. The radius of curvature of the trajectory, when it makes an angle ((theta)/(2)) with the horizontal is (g-acceleration due to gravity)
View SolutionA particle is projected with initial speed u at an angle theta above the horizontal . Let A be the point of projection , B the point where velocity makes an angle theta //2 above the horizontal and C the highest point of the trajectory . Radius of curvature of the trajectory at point A is
View SolutionA particle is projected with initial speed u at an angle theta above the horizontal . Let A be the point of projection , B the point where velocity makes an angle theta //2 above the horizontal and C the highest point of the trajectory . Radius of curvature of the trajectory at point B is
View SolutionA particle is projected with initial speed u at an angle θ above the horizontal . Let A be the point of projection , B the point where velocity makes an angle θ/2 above the horizontal and C the highest point of the trajectory .
Radius of curvature of the trajectory at point C is
View SolutionFrom a projectile horizontal theta The angle v is projected at velocity. What will be the speed of this projectile when it is relative to the horizontal direction beta Which angle are you on?
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle theta with the horizontal, at a point where the velocity of particle makes an angle theta//2 with the horizontal.
View Solution

