y(x,t)=0.8[(4x+5t)2+5] represents a moving pulse where x and y are in metre and t in second. Then,choose the correct alternative(s):
(a) pules is moving in positive x- direction
(b) in 2s it will travel a distance of 2.5m
(c) its maximum displacement is 0.16m
(d) it is a sysmmetric pulse
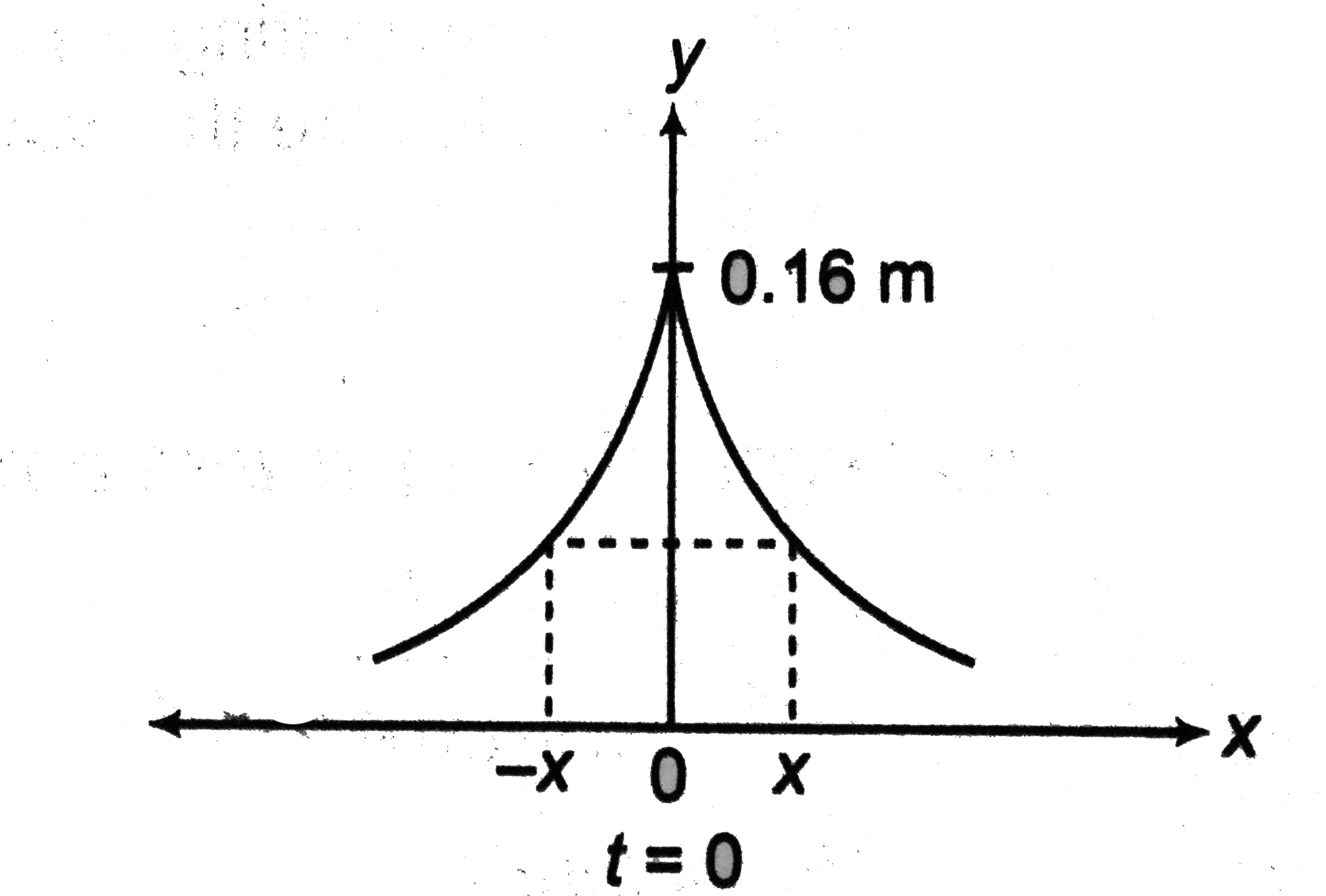
pulse is moving in + x-direction
in 2s it will travel a distance of 2.5m
its maximum displacement is 0.16m
it is a symmetric pulse
The correct Answer is:B, C, D
Given
y=0.8(4x+5t)2+5=0.816[x+54t]2+5….(i)
We know that equation of moving pulse is
y=f(x+vt)…(ii)
On comparing Eqs. (i) and (ii), we get
v=54m/s=2.52m/s
Wave will travel a distance of 2.5m in 2s.
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Comprehension
11 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Single Correct
51 Videos
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Integer
4 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
Similar Questions
Waves y1=Acos(0.5πx−100πt) and y2=Acos(0.46πx−92πt) are travelling along x-axis. (Here x is in m and t is in second)
(1) Find the number of times intensity is maximum in time interval of 1sec.
View SolutionA 20cm long string, having a mass of 1.0g, is fixed at both the ends. The tension in the string is 0.5N. The string is into vibrations using an external vibrator of frequency 100Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA cylindrical tube, open at both ends, has a fundamental frequency, f, in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air-column is now
View SolutionA metal rod AB of length 10x has its one end A in ice at 0∘C, and the other end B in water at 100∘C. If a point P one the rod is maintained at 400∘C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540cal/g and latent heat of melting of ice is 80cal/g. If the point P is at a distance of λx from the ice end A, find the value λ. [Neglect any heat loss to the surrounding.]
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
View Solutiony(x,t)=0.8/[4x+5t)2+5] represents a moving pulse, where x and y are in meter and t in second. Then
View Solutiony(x, t) =(0.8)/([(4x + 5t)^(2) +5]) represents a moving pulse where x and y are in metre and t in second. Then,choose the correct alternative(s): (a) pules is moving in positive x- direction (b) in 2 s it will travel a distance of 2.5 m (c) its maximum displacement is 0.16 m (d) it is a sysmmetric pulse
View Solutiony(x,t)=1.0[(ax+bt)2+(cx+dt)2+5] represents a moving pulse where x and y are in metres and t in seconds. It has speed of pulse b/a. Find the correct option.
View Solutionx(x,t)=0.8[(4x+5t)2+5], represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.
View Solutiony(x,t)=0.8[(4x+5t)2+5] एक गतिमान स्पन्द को व्यक्त करती है , जहाँ x तथा y मीटर में व t सेकण्ड में है। तब ,
View Solutionx(x,t)=0.8[(4x+5t)2+5], represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.
View SolutionAt t=0 , a transverse were pulse in a wire is described by the function where x and y are in metre. The function y(x, t) that describes this wave equation, if it is travelling in the positive x - direction with a speed of "4.5 m s"^(-1) is
View Solutiony(x,t) = (0.8)/([(4x + 5t)^2 + 5]) represents a moving pulse, where x and y are in metres and t' is in seconds, then
View SolutionY(x,t)=0.8[(4x+5t)2+5] represents a moving pulse where x and y are in metre and t is in second. Then
View Solutiony,(x,t)=0.8/[(4x+5t)2+5] represents a moving pulse, where x,y are in metre and t in second. then
View Solutiony(x,t) = 0.8/[((4x + 5t)^(2) +5)] represents a moving pulse, where x and y are in metres and .t. is in seconds, then
View Solution

