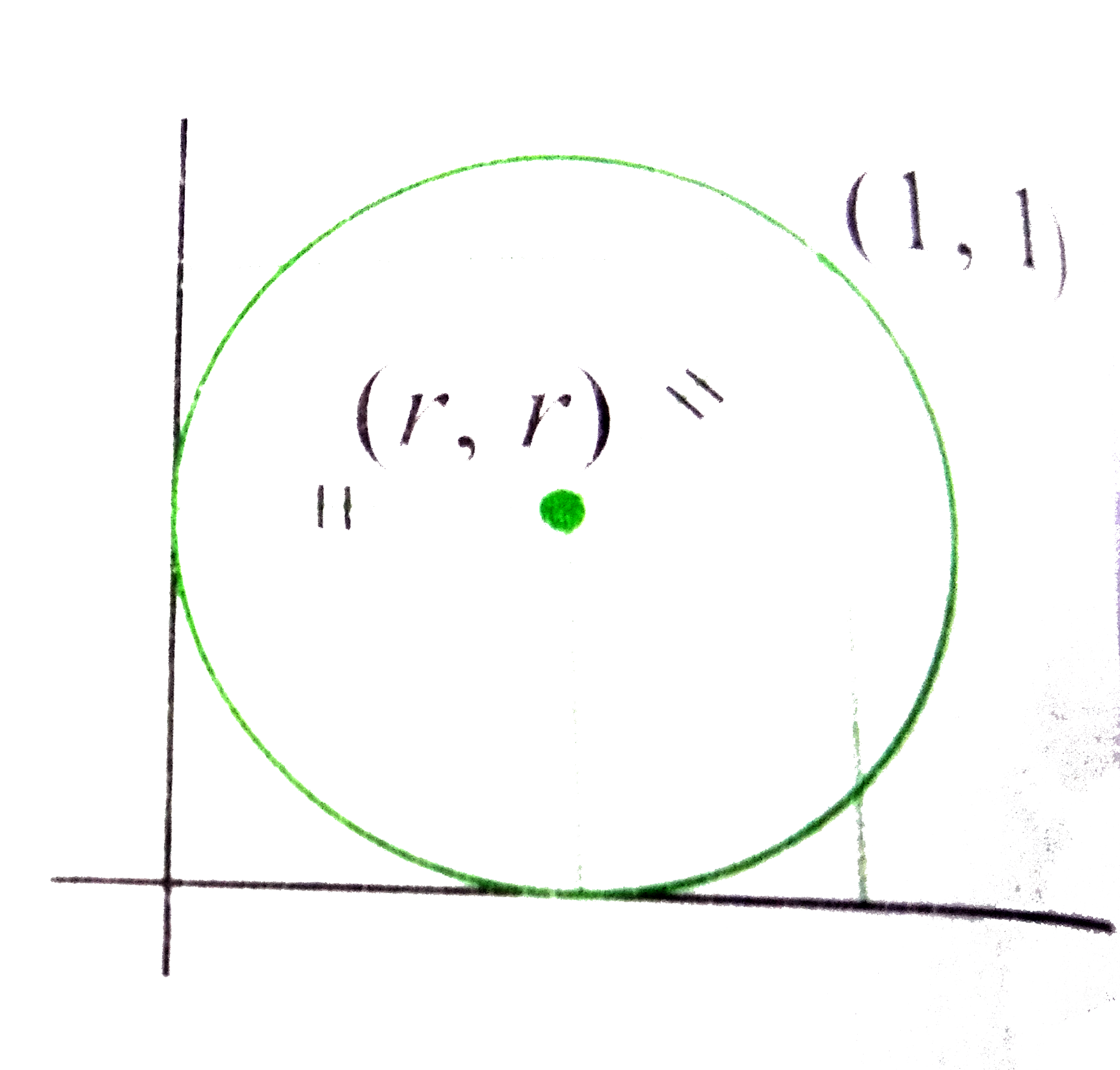
ABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is (a) 2−√2 (b) √2−1 (c) √2−12 (d) 1√2Solution in Bengali
2−√2
√2−1
1/2
1√2
The correct Answer is:1
From the figure,
2(1−r)2=r2
or √2(1−r)=r
or r(√2+1)=√2
or r=√2√2+1=√2(√2−1)=2−√2
Topper's Solved these Questions
- CIRCLE Book:CENGAGE PUBLICATIONChapter:CIRCLE Exercise:Multiple Correct Anser Type
Explore 17 Videos
- CIRCLE Book:CENGAGE PUBLICATIONChapter:CIRCLE Exercise:For Problems
Explore 7 Videos
- CIRCLE Book:CENGAGE PUBLICATIONChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.9
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE PUBLICATIONChapter:BINOMIAL THEOREMExercise:Comprehension
Explore 11 Videos
- CIRCLESBook:CENGAGE PUBLICATIONChapter:CIRCLESExercise:Comprehension Type
Explore 6 Videos
Similar Questions
Tangent drawn from the point (a,3) to the circle 2x2+2y2−25 will be perpendicular to each other if α equals 5 (b) −4 (c) 4 (d) −5
View SolutionTangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
View SolutionThe radius of the circle touching the line 2x+3y+1=0 at (1,-1) and cutting orthogonally the circle having line segment joining (0, 3) and (-2,-1) as diameter is
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionThe centre of a circle passing through (0,0),(1,0) and touching the Circle x^(2)+y^(2)=9 is a a ((1)/(2),sqrt(2)) b.((1)/(2),(3)/(sqrt(2))) c.((3)/(2),(1)/(sqrt(2))) d.((1)/(2),-(1)/(sqrt(2)))
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is 2−√2 (b) √2−1 1/2 (d) 1√2
View SolutionLet C be a circle with two diameters intersecting at an angle of 300. A circle S is tangent to both the diameters and to C and has radius unity. The largest radius of C is 1+√6+√2 (b) 1+√6−√2 √6+√2−11 (d) none of these
View SolutionThe line y=x is tangent at (0, 0) to a circle of radius 1. The centre of circle may be:
(a) (1√2,−1√2)
(b) (−12,12)
(c) (12,−12)
(d) (−1√2,1√2)
View SolutionLet C be the circle with centre (1,1) and radius 1.If T is the circle centered at (0,k) passing through origin and touching the circle C externally then the radius of T is equal to (a) √3√2 (b) √32 (c) 12 (d) 14
View SolutionA circle is circumscribed around a square as shown in the figure. The area of one of the four shaded portions is equal to 47 . The radius of the circle is (FIGURE) √2 (b) 1√2 (c) 2 (d) 3
View SolutionTangents drawn from (2,0) to the circle x2+y2=1 touch the circle at AandB. Then (A) A≡(12,√32), B -= (-1/2, - sqrt(3)/2)(B)A-= (- 1/2, (-sqrt(3)/2),B≡(12,√32) (C) A≡(12,√32), B-= (1/2, - sqrt(3)/2) (D) A≡(12,−√32),B≡(12,√32)
View SolutionIf a:b=c:d , then prove that (a+c):(b+d)=√a2−c2:√b2−d2
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is (a) 2−√2 (b) √2−1 (c) √2−12 (d) 1√2
View SolutionLet C be a circle with two diameters intersecting at an angle of 300. A circle S is tangent to both the diameters and to C and has radius unity. The largest radius of C is (a) 1+√6+√2 (b) 1+√6−√2 (c) √6+√2−11 (d) none of these
View SolutionA circle S of radius 'a' is the director circle of another circle S1,S1 is the director circle of circle S2 and so on. If the sum of the radii of all these circle is 2, then the value of 'a' is (a) 2+√2 (b) 2−1√2 (c) 2−√2 (d) 2+1√2
View Solution
