A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
150∘
180∘
160∘
170∘
The correct Answer is:A
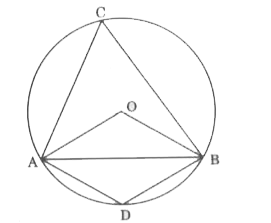
∠ACB is the angle subtended by chord AB on the major are
∠AOB is a equateral triangle
AB=AO=OB ∠AOB=600
∠ACB=12∠AOB
∠ACB=12⋅600=300
angle subtended by are ACB at centre
=reflex∠AOB
=3600−600=3000
∠ADB=1/2*reflex∠AOB
=1/2*300=1500.
Similar Questions
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionIf the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is .........
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.
View Solution
