A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs 8 per 100 cm2. (takeπ = 3.14)
The correct Answer is:Rs 156.75
To solve the problem, we need to find two things: the volume of the frustum of the cone (which will give us the amount of milk it can hold) and the surface area of the frustum (which will help us calculate the cost of the metal sheet used to make the container).
Step 1: Calculate the Volume of the Frustum of the Cone
The formula for the volume V of a frustum of a cone is given by:
V=13πh(r21+r22+r1r2)
Where:
- h is the height of the frustum,
- r1 is the radius of the lower base,
- r2 is the radius of the upper base.
Given:
- h=16cm
- r1=8cm
- r2=20cm
Substituting the values into the formula:
V=13×3.14×16×(82+202+8×20)
Calculating the squares and product:
82=64,202=400,8×20=160
Now, substituting these values:
V=13×3.14×16×(64+400+160)
=13×3.14×16×624
Calculating the sum:
64+400+160=624
Now calculating the volume:
V=13×3.14×16×624
=13×3.14×9984
=13×31376.16
=10458.72cm3
Step 2: Convert Volume to Liters
Since 1liter=1000cm3:
Volume in liters=10458.721000=10.45872liters
Step 3: Calculate the Cost of Milk
The cost of milk is given as Rs 20 per liter. Therefore, the total cost for the milk is:
Cost of milk=10.45872×20=209.1744≈209.17Rs
Step 4: Calculate the Curved Surface Area of the Frustum
The formula for the curved surface area A of a frustum of a cone is given by:
A=π(r1+r2)l
Where l is the slant height, which can be calculated using the Pythagorean theorem:
l=√(r2−r1)2+h2
Calculating l:
l=√(20−8)2+162=√122+162=√144+256=√400=20cm
Now substituting into the surface area formula:
A=3.14×(8+20)×20
=3.14×28×20
=3.14×560
=1758.4cm2
Step 5: Calculate the Cost of the Metal Sheet
The cost of the metal sheet is Rs 8 per 100 cm². Therefore, the total cost for the metal sheet is:
Cost of metal sheet=1758.4100×8=140.672≈140.67Rs
Final Answers
- Cost of milk: Rs 209.17
- Cost of metal sheet: Rs 140.67
- h is the height of the frustum,
- r1 is the radius of the lower base,
- r2 is the radius of the upper base.
- h=16cm
- r1=8cm
- r2=20cm
=13×3.14×16×624
=13×3.14×9984
=13×31376.16
=10458.72cm3
=3.14×28×20
=3.14×560
=1758.4cm2
- Cost of milk: Rs 209.17
- Cost of metal sheet: Rs 140.67
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - NCERT SECTION (EXERCISE 13.5)
7 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS)
50 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - NCERT SECTION (EXERCISE 13.3)
9 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
12 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
Similar Questions
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8. 88g"\ "p e r"\
View SolutionThe volume of a cube is 2744cm3 . Its surface area is
View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
View SolutionThe average score of Sehwag in 10 innings was 77 runs. In the 11th inning he had scored zero runs. The overall average score of Sehwag in all the 11 innings was
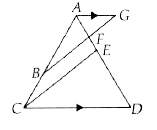
View SolutionIn the given figure (not drawn to scalse ) , AG is parallel to CD and AG=27CD . The point B on AC is such that BC=27AC . If the line BG meets AD at F and the line through C is parallel to BG which meets AD at E , then find the value of FGEC .
View SolutionA milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of milk at the rate of ₹22 per L which the container can hold.
View SolutionA container made of a metal sheet open at the top is the form of frustum of the cone, whose height is 16 cm and the radii of its lower and upper circular edges are 8 cm and 20 cm respectively. Find
(i) the cost of metal sheet to make the container if it costs ₹ 10 per 100cm2
(ii) the cost of milk at the rate of ₹ 35 per litre which can fill it completely.
View SolutionA bucket made up of a metal sheet is in the form of a frustum of cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the bucket if the cost metal sheet used is ₹ 15 per 100cm2. [ Use π=3.14]
View Solutiona container open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 14 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. find the capacity of the container.
View Solutionधातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है , जिसकी ऊंचाई 16 सेमी है तथा नीचले और ऊपरी सिरों की त्रिज्याएँ क्रमश: 8 सेमी और 20 सेमी है । रु 20 प्रति लीटर की दर से , इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए । साथ ही , इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य रु 8 प्रति 100सेमी2 की दर से ज्ञात कीजिए । (π=3.14 लीजिए )
View SolutionA container open at the top is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the cost of milk which can completely fill a container at the rate of Rs. 40 per litre.
View SolutionA container opened at the top and made up of a meta! sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ? 50 per litre. Also find the cost of meta! sheet used to make the container, if it costs Rs. 10 per 100cm2 ? ( Take π = 3.14).
View Solutiona container open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 14 cm with radii of its lower and upper circular ends as 6 cm and 21 cm, respectively. find the capacity of the container.
View SolutionA milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of milk at the rate of ₹22 per L which the container can hold.
View SolutionA container open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 14 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. find the capacity of the container.
View SolutionA milk container is made of metal sheet in the shape of frustum of a cone whose volume is 1045937cm2. The radii of its lower and upper circular ends are 8 cm and 20 cm respectively. Find the cost of metal sheet used in making the container at the rate of Rs. 1.40 per square centimeter.
View Solution
