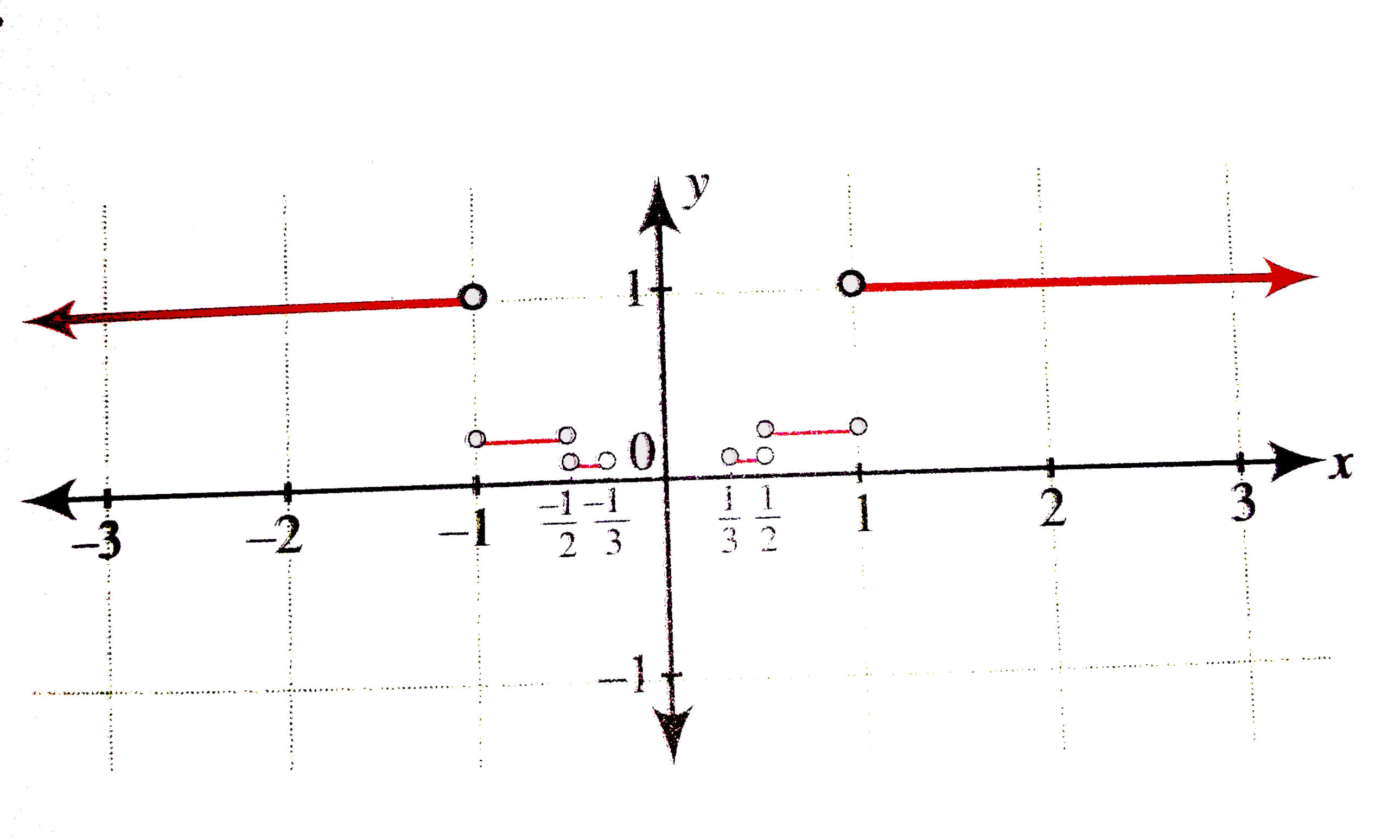
(a) Draw the graph of f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3.
Text Solution
(a) f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩1,x≤−1orx≥114,x∈(−1,−12)∪(12,1)19,x∈(−12,−13)∪(13,12)...
(b) y≤−1
For y≤−1, first draw the line y=−1. All the points satisfying y≤−1 have ordinate greater than, or equal to, -1, i.e. all the points lying on or below the line y=−1.
The region is as shown in the following region.

(c ) |x|<3
So −3<x<3, i.e. all points have abscissae lying between -3 and 3. Hence all the points lying between the lines x=−3andx=3.

|
Similar Questions
Sketch the graph of y=sin(13x) for 0≤x<6π.
View SolutionThe number of real roots of :
1+a1X+a2x2....+anxn=0, where |x|<13 and |an|<2, is :
View Solution(a) Draw the graph of f(x)==⎧⎪ ⎪⎨⎪ ⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3.
View Solutionf(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩12−x,0≤x<121,x=1232−x,12<x≤1 Discuss the continuity of f(x)
View Solutionf(x)=⎧⎪⎨⎪⎩[x]if−3<x≤−1|x|if−1<x<1|[−x]|if1≤x≤3, then {x:f(x)≥0}=
View SolutionIf f(x)=xn for 0<a<b and nan−1≤bn−anb−a≤nbn−1 then n is
View SolutionIf f(x)={:{(x", for " 0 le x lt 1),(2", for " x=1),(x+1", for " 1 lt x le 2):} , then f is
View SolutionIf 0<x<π2 and sinnx+cosnx≥1, then
View Solution

