A random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
725
1825
1325
1625
The correct Answer is:D
P(X=0)=k,P(X=1)=2k(15)1
P(X=2)=3k(15)2...=1
Since P(X=0)+P(X=1)+P(X=2)+...=1
∴k+2k(15)+3k(15)2+...=1
andk5+2k(15)2+...=15k+k(15)+k(15)2+...=45
⇒ k1−15=45⇒k=1625
∴ P(X=0)=1625(0+1)(15)0=1625
Topper's Solved these Questions
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 40 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:MHT CET Corner
Explore 4 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
Explore 30 Videos
- PRACTICE SET 24Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 24Exercise:Paper 2 (Mathmatics)
Explore 50 Videos
- SEQUENCES AND SERIES Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SEQUENCES AND SERIES Exercise:EXERCISE 31
Explore 1 Video
Similar Questions
If a random variable X has the following probability distribution values of X
Then P(X≥6) is equal to

View SolutionIf a random variable waiting time in minutes for bus and probability density function of x is given by
f(x)={15,0≤x≤50,otherwise
Then probability of waiting time not more than 4 minutes is equal to
View SolutionTwo dice are thrown simultaneously. the probability of obtaining a total score of 5 is a. 1/18 b. 1/12 c. 1/9 d. none of these
View SolutionThe switching function for the following network is
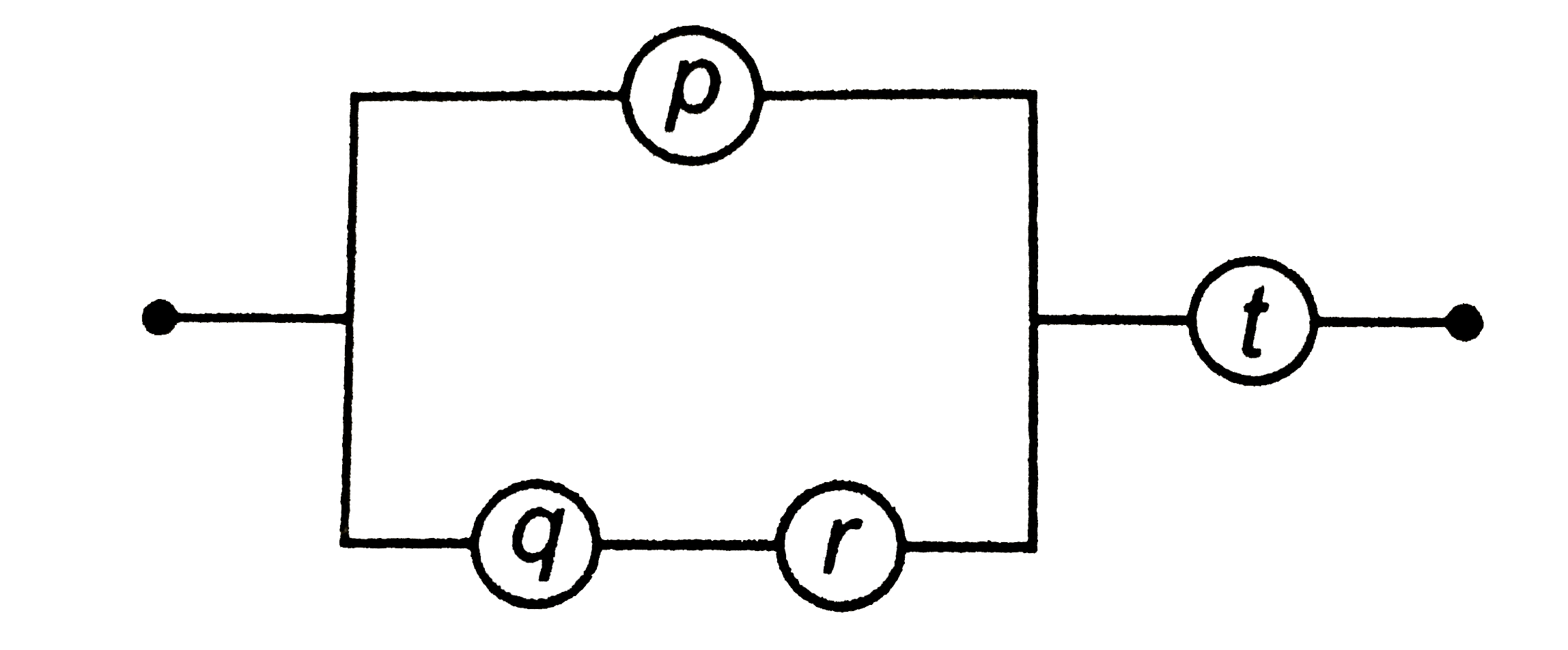
View SolutionThe coefficient of x3 in the expansion of 3x is
View SolutionIf the range ot a random vaniabie X is 0,1,2,3, at P(X=K)=(K+13k) a for k≥0, then a equals
View SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionIf X is a random -variable with distribution given below :
x:0123p(x):k3k3kk
The value of k and its variance are
View SolutionX is a random variable with distribution given below
x:0123P(X=x):k3k3kk
The value of k and its variance are
View SolutionIf a discrete random variable can take only the values 0,1,2,3, the probability mass function is given by f(x)={k(x2+x+1),x=0,1,2,30,otherwise Find K
View SolutionIf a discrete random variable can take only the values 0,1,2,3, the probability mass function is given by f(x)={k(x2+x+1),x=0,1,2,30,otherwise Find cumulative distribution function
View SolutionIf a discrete random variable can take only the values 0,1,2,3, the probability mass function is given by f(x)={k(x2+x+1),x=0,1,2,30,otherwise Find Mean of the distribution .
View SolutionIf the probability function of a random variable X is defined by P(X=k)=a(k+12k) for k=0,1,2,3,4,5, then the probability that X takes a prime value is
View SolutionA random variable X takes the values 0,1,2,3,...,
with prbability P(X=x)=k(x+1)(15)x, where k is a constant,
then P(X=0) is.
View SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionIf the range of a random variable X is {0,1,2,3 …..,} with P(X=k)=((k+1))a3k for k≥0, then a =
View Solution
