A rectangular tank has length = 4 m, width = 3 m and capacity = 30m3. A small model of the tank is made with capacity 240cm3. Find :
the dimensions of the model.
The correct Answer is:8cm×6cm×5cm
To find the dimensions of the small model of the rectangular tank, we will follow these steps:
Step 1: Find the height of the original tank.
We know the volume of the rectangular tank is given by the formula:
Volume=Length×Width×Height
Given:
- Length L=4m
- Width W=3m
- Volume V=30m3
We can rearrange the formula to find the height H:
H=VL×W=304×3=3012=2.5m
Step 2: Determine the scale factor for the model.
The volume of the model is given as 240cm3. First, we need to convert the dimensions of the original tank from meters to centimeters since the model's volume is in cubic centimeters.
- Length L=4m=400cm
- Width W=3m=300cm
- Height H=2.5m=250cm
Let the scale factor be k. The dimensions of the model will be:
- Length of the model = 400k
- Width of the model = 300k
- Height of the model = 250k
Step 3: Set up the equation for the volume of the model.
The volume of the model can also be expressed as:
Volume=Length×Width×Height
Substituting the dimensions of the model:
240=(400k)×(300k)×(250k)
This simplifies to:
240=400×300×250×k3
Step 4: Calculate k3.
Calculating the constant:
400×300=120000
120000×250=30000000
Now we have:
240=30000000×k3
Rearranging gives:
k3=24030000000=24030000000=1125000=0.00000192
To simplify:
k3=1125⇒k=√(3)1125=15
Step 5: Find the dimensions of the model.
Now we can find the dimensions of the model:
- Length of the model = 400k=400×15=80cm
- Width of the model = 300k=300×15=60cm
- Height of the model = 250k=250×15=50cm
Final Answer:
The dimensions of the model are:
Length=80cm,Width=60cm,Height=50cm
---
We know the volume of the rectangular tank is given by the formula:
Volume=Length×Width×Height
Given:
- Length L=4m
- Width W=3m
- Volume V=30m3
H=VL×W=304×3=3012=2.5m
The volume of the model is given as 240cm3. First, we need to convert the dimensions of the original tank from meters to centimeters since the model's volume is in cubic centimeters.
- Length L=4m=400cm
- Width W=3m=300cm
- Height H=2.5m=250cm
- Length of the model = 400k
- Width of the model = 300k
- Height of the model = 250k
The volume of the model can also be expressed as:
Volume=Length×Width×Height
Substituting the dimensions of the model:
240=(400k)×(300k)×(250k)
This simplifies to:
240=400×300×250×k3
Calculating the constant:
400×300=120000
120000×250=30000000
Now we have:
240=30000000×k3
Rearranging gives:
k3=24030000000=24030000000=1125000=0.00000192
To simplify:
k3=1125⇒k=√(3)1125=15
Now we can find the dimensions of the model:
- Length of the model = 400k=400×15=80cm
- Width of the model = 300k=300×15=60cm
- Height of the model = 250k=250×15=50cm
The dimensions of the model are:
Length=80cm,Width=60cm,Height=50cm
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(A)
Explore 48 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(B)
Explore 17 Videos
- SIMILARITY Book:ICSEChapter:SIMILARITY Exercise:MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
Explore 10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Book:ICSEChapter:SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Exercise:Exercise 6(e )
Explore 18 Videos
Similar Questions
In the figure, given below, straight lines AB and CD intersect at P, and AC//BD. Prove that :

ΔAPCandΔBPD are similar.
View SolutionIn the following figure, point D divides AB in the ratio 3: 5. Find :
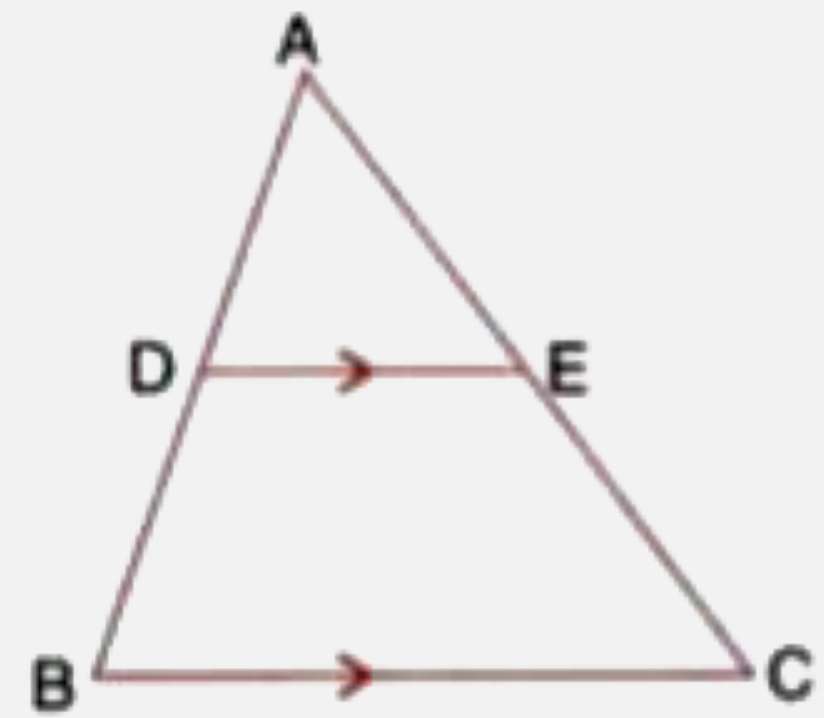
AEEC
View SolutionA girl, named Ritika of height 90 cm is walking away from the ase of a lamp-post, She observes the shadows of lamp-post and herself and relate it with a chapter of mathematics, she studied in her last class.
On the basis of information, answer the following question
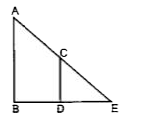
The triangles ABE and CDE are similar by which of the following similarity rule ?
View SolutionThe distance between two towns A and B is 216 km, and by rail it is 208 km. A car travels at a speed of xkm/hr and the train travels at a speed which is 16km/hr faster than the car. Calculate :
(i) the time taken by the car to reach town B from A, in terms of x,
(i) the time taken by ht etrain, to reach town B from A, in terms of .
(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x, and solve it.
(iv) Hence, find the speed of the train.
View SolutionInner measurements of a rectangular water tank are 6 m long, 3 m wide, and 2 m depth, then the capacity of the tank is ______.
View Solutionएक घनाभाकर टंकी की धारिता 50000 लीटर पाने की है | यदि इस टंकी की लंबाई और गहराई क्रमश : 2.5 m और 10 m है, तो इसकी चौड़ाई ज्ञात कीजिए |
View SolutionFind the capacity of a cuboidal tank in litres if its dimensions are 3 m xx 2.2 m xx 1.6 m
View Solutionधनाभ के आकार की एक पानी की टंकी की धारिता 13,500 लीटर है। यदि टंकी की लम्बाई और चौड़ाई क्रमशः 1.5 मीटर और 1.2 मीटर हों, तो टंकी की ऊँचाई ज्ञात कीजिए
View Solutionಆಯತ ಘನಾಕಾರದ ಒಂದು ನೀರಿನ ತೊಟ್ಟಿಯ ಸಾಮರ್ಥ್ಯವು 50,000 ಲೀಟರ್ ಆಗಿದೆ. ಅದರ ಉದ್ದ ಮತ್ತು ಅಳವು ಕ್ರಮವಾಗಿ 10 m ಮತ್ತು 2.5 m ಆದರೆ ಅದರ ಅಗಲವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionAn overhead water tanker is in the shape of a cylinder has capacity of 61.6m3. The diameter of the tank is 5.6m. Find the height of the tank.
View SolutionA cylindrical tank has a capacity of 6160 m3. Find its depth, if the diameter of its base is 28 m.
View Solutionपानी के एक घनाभकार टैंक की क्षमता 50000 लीटर है, तब टैंक की चौड़ाई ज्ञात कीजिए, यदि इसकी लम्बाई और गहराई क्रमशः 2.5 मी तथा 10 मी है
View SolutionThe internal dimensions of a water tank are 2.4 m by 1.6 m by 1.2 m Find the capacity of the tank in litres.
View SolutionThe length, breadth and height of a water tank are 5 m, 2.5 m and 1.25 m respectively. Calculate the capacity of the water tank in m^3
View Solutionਇਕ ਘਣਾਵਕਾਰ ਟੈਂਕੀ ਦੀ ਸਮਰਥਾ 50000 ਲਿਟਰ ਪਾਣੀ ਦੀ ਹੈ। ਜੇਕਰ ਟੈਂਕੀ ਦੀ ਲੰਬਾਈ ਅਤੇ ਡੂੰਘਾਈ ਕ੍ਰਮਵਾਰ 2.5 ਮੀ. ਅਤੇ 10 ਮੀ. ਹੋਵੇ ਤਾਂ ਚੌੜਾਈ ਪਤਾ ਕਰੋ।
View Solution