A right angled triangle ABC of sides AB=6, BC=8 and AC=10 is spun once about AB and once about BC. What is the difference in volumes of the two solids formed?
24π
32π
64π
96π
The correct Answer is:B
To solve the problem, we need to find the volumes of the solids formed when the right-angled triangle ABC is spun about sides AB and BC, and then calculate the difference between these two volumes.
1. Identify the Triangle and Its Dimensions:
- We have a right-angled triangle ABC with sides:
- AB = 6 (height when spun around AB)
- BC = 8 (radius when spun around AB)
- AC = 10 (hypotenuse)
2. Volume of the Solid Formed by Spinning Around AB:
- When the triangle is spun around side AB, it forms a cone.
- The formula for the volume V of a cone is:
V=13πr2h
- Here, the radius r is BC = 8 and the height h is AB = 6.
- Substitute the values into the formula:
V1=13π(8)2(6)
- Calculate V1:
V1=13π(64)(6)=13π(384)=128π
3. Volume of the Solid Formed by Spinning Around BC:
- When the triangle is spun around side BC, it also forms a cone.
- Here, the radius r is AB = 6 and the height h is BC = 8.
- Substitute the values into the formula:
V2=13π(6)2(8)
- Calculate V2:
V2=13π(36)(8)=13π(288)=96π
4. Calculate the Difference in Volumes:
- Now, we find the difference between the two volumes:
Difference=V1−V2=128π−96π=32π
Final Answer:
The difference in volumes of the two solids formed is 32π.
- We have a right-angled triangle ABC with sides:
- AB = 6 (height when spun around AB)
- BC = 8 (radius when spun around AB)
- AC = 10 (hypotenuse)
- When the triangle is spun around side AB, it forms a cone.
- The formula for the volume V of a cone is:
V=13πr2h
- Here, the radius r is BC = 8 and the height h is AB = 6.
- Substitute the values into the formula:
V1=13π(8)2(6)
- Calculate V1:
V1=13π(64)(6)=13π(384)=128π
- When the triangle is spun around side BC, it also forms a cone.
- Here, the radius r is AB = 6 and the height h is BC = 8.
- Substitute the values into the formula:
V2=13π(6)2(8)
- Calculate V2:
V2=13π(36)(8)=13π(288)=96π
- Now, we find the difference between the two volumes:
Difference=V1−V2=128π−96π=32π
The difference in volumes of the two solids formed is 32π.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Grib-In
Explore 32 Videos
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- COMPLEX NUMBERSBook:ENGLISH SATChapter:COMPLEX NUMBERSExercise:EXERCISE
Explore 6 Videos
Similar Questions
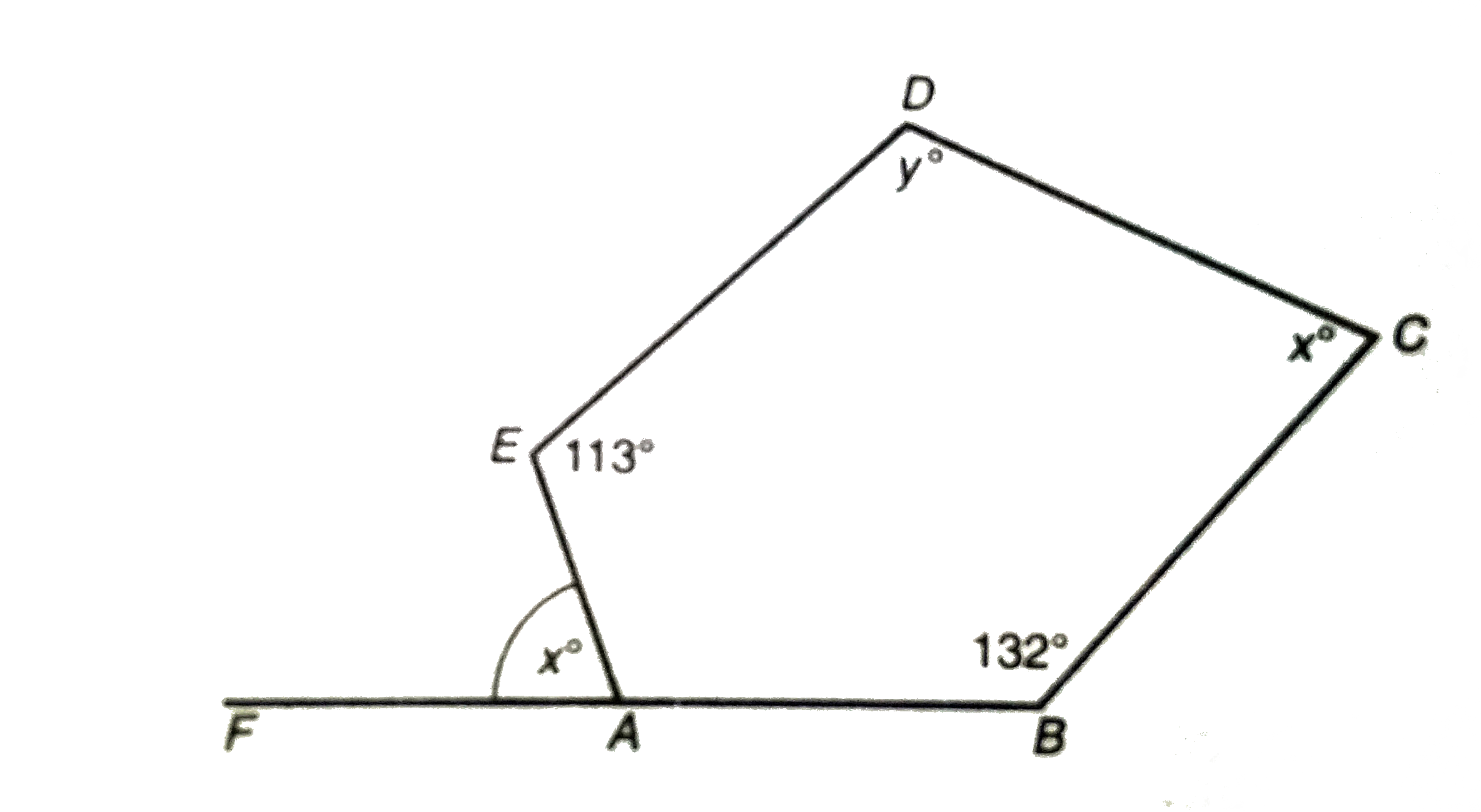
In the accompaying figure of pentagon ABCDE, points F, A, and B lie on the same line. What is the value of y?
View SolutionA rectangular box with length 22 inches , width 5 inches , and height 5 inches is to be packed with steel balls of radius 2 inches in such a way that the centers of the balls are collinear. What is the maximum number of balls that can fit into the box, provided that no balls should protrude from the box ?
View Solutioni29=
View SolutionDelta ABC is a right triangle right angled at A such that AB=AC and bisector of /_C intersects the side AB at D.Prove that AC+AD=BC .
View SolutionIn right triangle, ABC, AB=10,BC=8,AC=6.
View SolutionIn a right-angled triangle ABC, right angled at B, an altitude BD is dropped on AC. If AB=8 and BC=6, what is the length of AD?
View SolutionIn △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
View SolutionIn ΔABC , right angle is at B,AB = 5cm and ∠ACB=30∘ Determine the lengths of the sides BC and AC.
View SolutionIn ΔABC , right angle is at B,AB = 5cm and ∠ACB=30∘ Determine the lengths of the sides BC and AC.
View SolutionIn ΔABC , right angle is at B,AB = 5cm and ∠ACB=30∘ Determine the lengths of the sides BC and AC.
View SolutionIn ΔABC , right angle is at B,AB = 5cm and ∠ACB=30∘ Determine the lengths of the sides BC and AC.
View SolutionIn ΔABC, right-angled at B, AB = 3 cm and ∠BAC =60∘ . Determine the lengths of the sides BC and AC.
View SolutionIn ΔABC , right angle is at B,AB = 5cm and ∠ACB=30∘ Determine the lengths of the sides BC and AC.
View SolutionΔABC में, AC = 10 सेमी., AB = 6 सेमी. और BC = 8 सेमी. है। क्या त्रिभुज समकोण है ?
View SolutionIn a right triangle ABC,∠B=90∘ : If AB = 6 cm, BC = 8 cm, find AC
View Solution
