A sphere and a right circular cylinder of the same radius have equal volume. By what percentage does the diameter of the cylinder exceed its height ?
To solve the problem step by step, we will follow the reasoning provided in the video transcript and derive the solution systematically.
Step 1: Understand the Problem
We have a sphere and a right circular cylinder with the same radius r and equal volumes. We need to find the percentage by which the diameter of the cylinder exceeds its height.
Step 2: Write Down the Volume Formulas
The volume V of a cylinder is given by:
Vcylinder=πr2h
The volume V of a sphere is given by:
Vsphere=43πr3
Step 3: Set the Volumes Equal
Since the volumes are equal, we can set the two equations equal to each other:
πr2h=43πr3
Step 4: Simplify the Equation
We can cancel π from both sides:
r2h=43r3
Now, divide both sides by r2 (assuming r≠0):
h=43r
Step 5: Find the Diameter of the Cylinder
The diameter d of the cylinder is given by:
d=2r
Step 6: Calculate the Percentage by Which the Diameter Exceeds the Height
We need to find the percentage by which the diameter exceeds the height:
Percentage=(d−hh)×100
Substituting the values of d and h:
Percentage=⎛⎝2r−43r43r⎞⎠×100
Step 7: Simplify the Expression
First, simplify the numerator:
2r−43r=63r−43r=23r
Now substitute this back into the percentage formula:
Percentage=⎛⎝23r43r⎞⎠×100
The r cancels out:
Percentage=(24)×100=12×100=50%
Final Answer
The diameter of the cylinder exceeds its height by 50%.
---
We have a sphere and a right circular cylinder with the same radius r and equal volumes. We need to find the percentage by which the diameter of the cylinder exceeds its height.
The volume V of a cylinder is given by:
Vcylinder=πr2h
The volume V of a sphere is given by:
Vsphere=43πr3
Since the volumes are equal, we can set the two equations equal to each other:
πr2h=43πr3
We can cancel π from both sides:
r2h=43r3
Now, divide both sides by r2 (assuming r≠0):
h=43r
The diameter d of the cylinder is given by:
d=2r
We need to find the percentage by which the diameter exceeds the height:
Percentage=(d−hh)×100
Substituting the values of d and h:
Percentage=⎛⎝2r−43r43r⎞⎠×100
First, simplify the numerator:
2r−43r=63r−43r=23r
Now substitute this back into the percentage formula:
Percentage=⎛⎝23r43r⎞⎠×100
The r cancels out:
Percentage=(24)×100=12×100=50%
The diameter of the cylinder exceeds its height by 50%.
Topper's Solved these Questions
Similar Questions
A right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View SolutionThe curved surface area of a right circular cylinder of height 14 cmis 88 cm2. Find the diameter of the base of the cylinder.
View Solution
Knowledge Check
If a right cylinder with a radius of 2 cm has a volume of 100πcm3, what is the height, in centimeters, of the cylinder?
A20B25C40D50The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
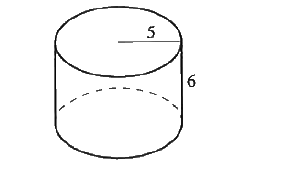 A30πB31πC150πD180π
A30πB31πC150πD180πIf a right circular cylinder of height 10 is inscribed in a sphere of radius 6, what is the volume of the cylinder ?
A104B346C545D785
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
View SolutionA rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diamter and height of the cylinder are 6 cm and 12 cm , respectively. If the slant height of the conical portion is 5 cm, the find the total surface area and volume of the rocket. ( use π=3.14).
View SolutionAn oil tank has the shape of a right circular cylinder is 12 centimeters in height and has a volume of 108π cubic centimeters. What is the diameter of the base of the cylinder, in centimeters?
View SolutionShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
View SolutionShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
View Solution