A tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L, perpendicular to PT is a tangent to the circle (x−3)2+y2=1 then find a common tangent of the two circles
x=4
y=2
x+√3y=4
x+2√2y=6
The correct Answer is:D
The point of intersection of direct common tangnets is (6,0)
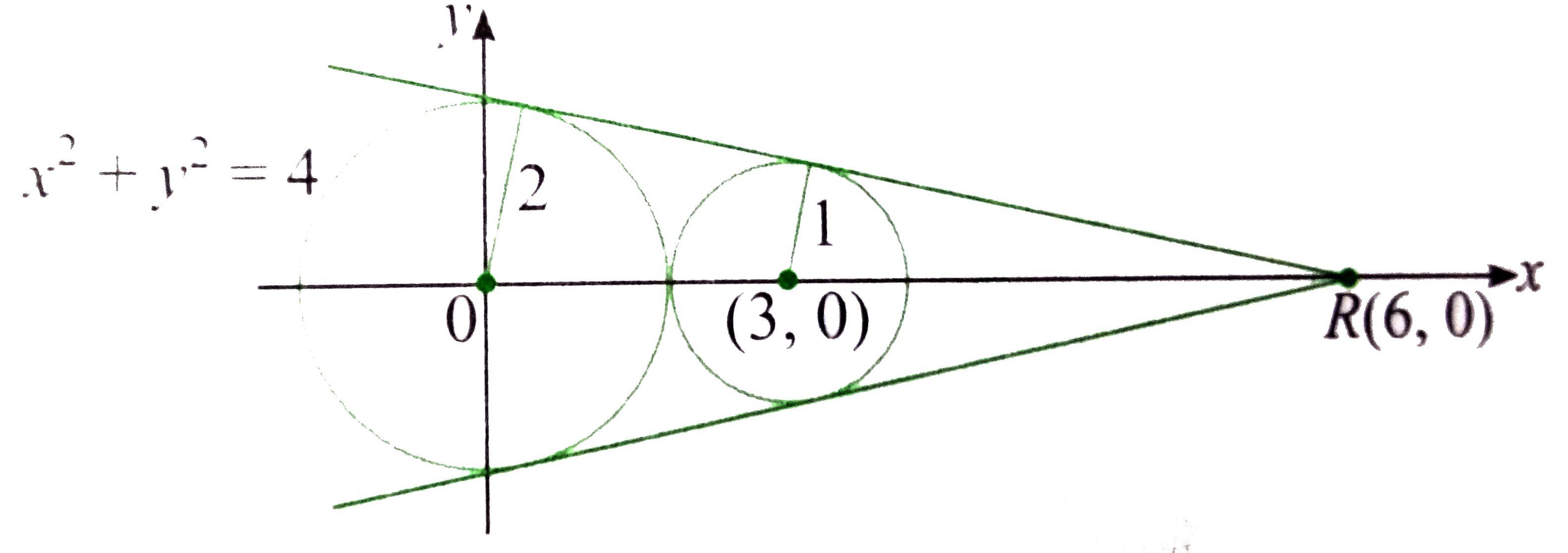
So, let the equation of common tangnet be
y−0=m(x−6)
As it touches x2+y2=4, we have
∣∣∣0−0−6m√1+m2∣∣∣=2
or 9m2=1+m2
or m=±12√2
So, the equation of common tangents are
y=12√2(x−6),y=−12√2(x−6) , also x=2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - JEE ADVANCED (Single Correct Answer Type)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
PARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionA tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L is perpendicular to PT is a tangent to the circle (x−3)2+y2=1 Common tangent of two circle is: (A) x=4 (B) y=2 (C) x+(√3)y=4 (D) x+2(√2)y=6
View SolutionFrom a pt A common tangents are drawn to a circle x^(2)+y^(2)=(a^(2))/(2) and y^(2)=4ax. Find the area of the quadrilateral formed by common tangents,chord of contact of circle and chord of contact of parabola.
View SolutionA tangent PT is drawn to the circle x^(2)+y^(2)=4 at the point P(sqrt(3),1). A straight line L, perpendicular to PT is a tangent to the circle (x-3)^(2)+y^(2)=1 then find a common tangent of the two circles
View SolutionA tangent PT is drawn to the circle x2+y2=4 at point p(√3,1) A straight line L perpendicular to PT is a tangent to the circle (x−3)2+y2=1 A possible equation of L is
View SolutionTangents are drawn from a point P on the line y=4 to the circle x^(2)+y^(2)=25 .If the tangents are perpendicular to each other,then coordinates of P are
View Solutionस्पर्श-रेखा PT वृत्त x2+y2=4 को बिन्दु P(√3,1) पर स्पर्श करती है। सरल रेखा L, PT के लम्बवत् है और वृत्त (x−3)2+y2=1 की स्पर्श-रेखा है।
दोनों वृत्तों की एक उभयनिष्ठ स्पर्श-रेखा (common tangent) निम्न है.
View Solutionस्पर्श-रेखा PT वृत्त x2+y2=4 को बिन्दु P(√3,1) पर स्पर्श करती है। सरल रेखा L, PT के लम्बवत् है और वृत्त (x−3)2+y2=1 की स्पर्श-रेखा है।
दोनों वृत्तों की एक उभयनिष्ठ स्पर्श-रेखा (common tangent) निम्न है.
View Solutionवृत्त x2+y2=2a2 तथा परवलय y2=8ax की दो उभयनिष्ठ स्पर्श रेखाओं का समीकरण है
View SolutionA tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L, perpendicular to PT is a tangent to the circle (x−3)2+y2=1 then find a common tangent of the two circles
View Solutionस्पर्श-रेखा PT वृत्त x2+y2=4 को बिन्दु P(√3,1) पर स्पर्श करती है। सरल रेखा L, PT के लम्बवत् है और वृत्त (x−3)2+y2=1 की स्पर्श-रेखा है।
दोनों वृत्तों की एक उभयनिष्ठ स्पर्श-रेखा (common tangent) निम्न है.
View Solutionस्पर्श-रेखा PT वृत्त x2+y2=4 को बिन्दु P(√3,1) पर स्पर्श करती है। सरल रेखा L, PT के लम्बवत् है और वृत्त (x−3)2+y2=1 की स्पर्श-रेखा है।
दोनों वृत्तों की एक उभयनिष्ठ स्पर्श-रेखा (common tangent) निम्न है.
View SolutionA tangent PT is drawn to the circle x^2+y^2 =4 at the point P(sqrt3,1) . A straight line L, perpendicular to PT is a tangent to the circle. (x - 3)^2+ y^2 = 1 A possible equation of L is
View Solution

