A vertical tower, OP stands at the center O of a square ABCD. Let h and b denote the length OP and AB respectively. If ∠APB=60∘, what is the relationship beween h and b?
2b2=h2
2h2=b2
3b2=2h2
3h2=2b2
The correct Answer is:B
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Grib-In
Explore 32 Videos
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- COMPLEX NUMBERSBook:ENGLISH SATChapter:COMPLEX NUMBERSExercise:EXERCISE
Explore 6 Videos
Similar Questions
The centre of a circle is at O. AB and CD are two chordsof length dande respectively. If P is the mid point of CD, then the length OP is:
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View Solution
Knowledge Check
A tower of height h stands at a point O on the ground. Two poles of height a and b stand at the points A and B respectively such that O lies on the line joining A and B. If the angle of elevation of the top of the tower at the foot of one pole is ame as at the top of the other pole, then h is equal to
Aa+babBaba+bCa + bDa+b|a−b|A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
Aa√3B√3aC2a√3D2√3aA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
A2a√3B2a√3Ca√3Da√3
In the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionConsider a triangle ABC and let a, b and c denote the lengths of the sides opposite to vertices A,B and C respectively. If a=1,b=3 and C=60∘, the sin2B is equal to
View Solution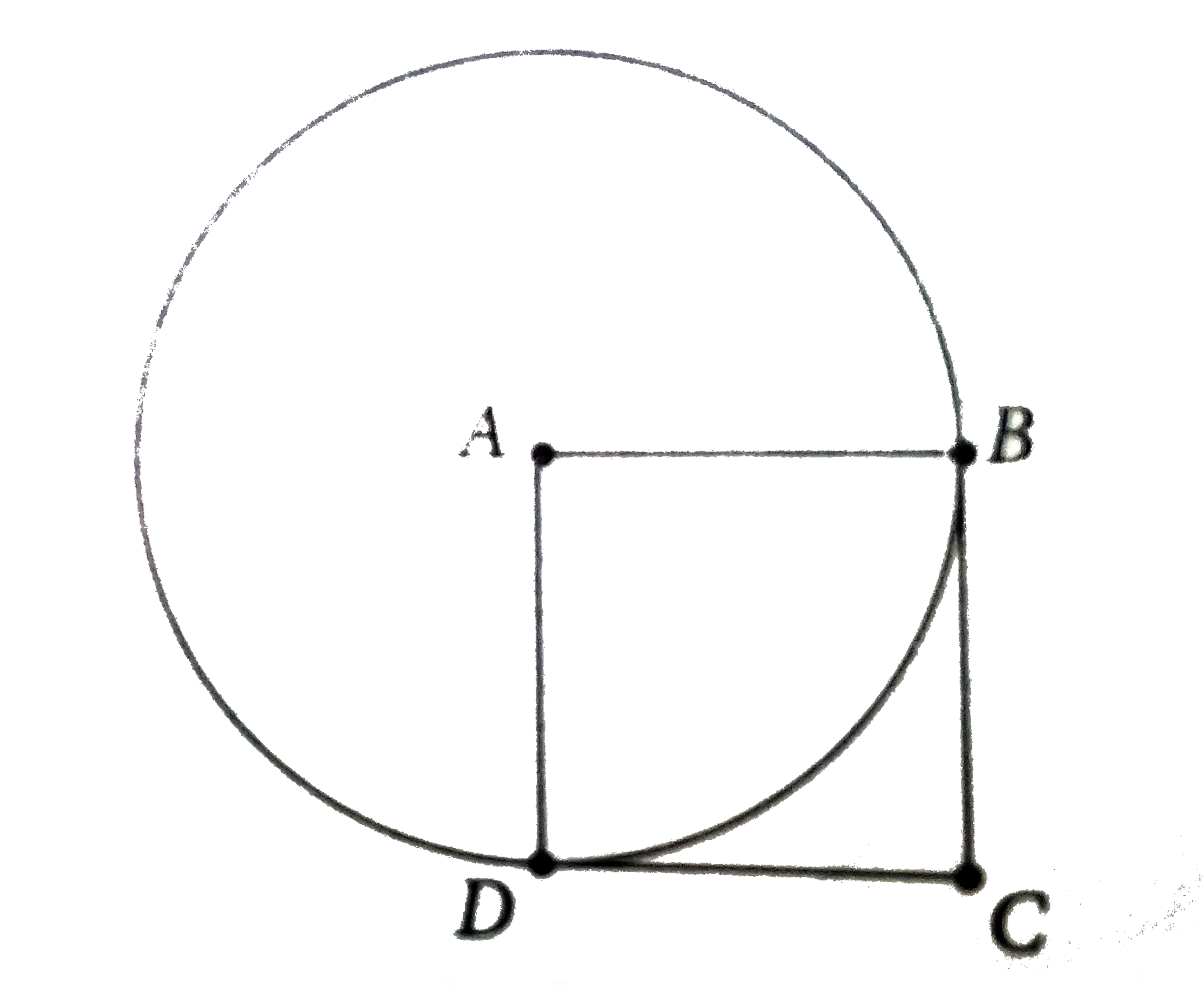
Points D and B lie on the circle above with center A. If square ABCD has an area of 16, what is the length of arc BD?
View Solution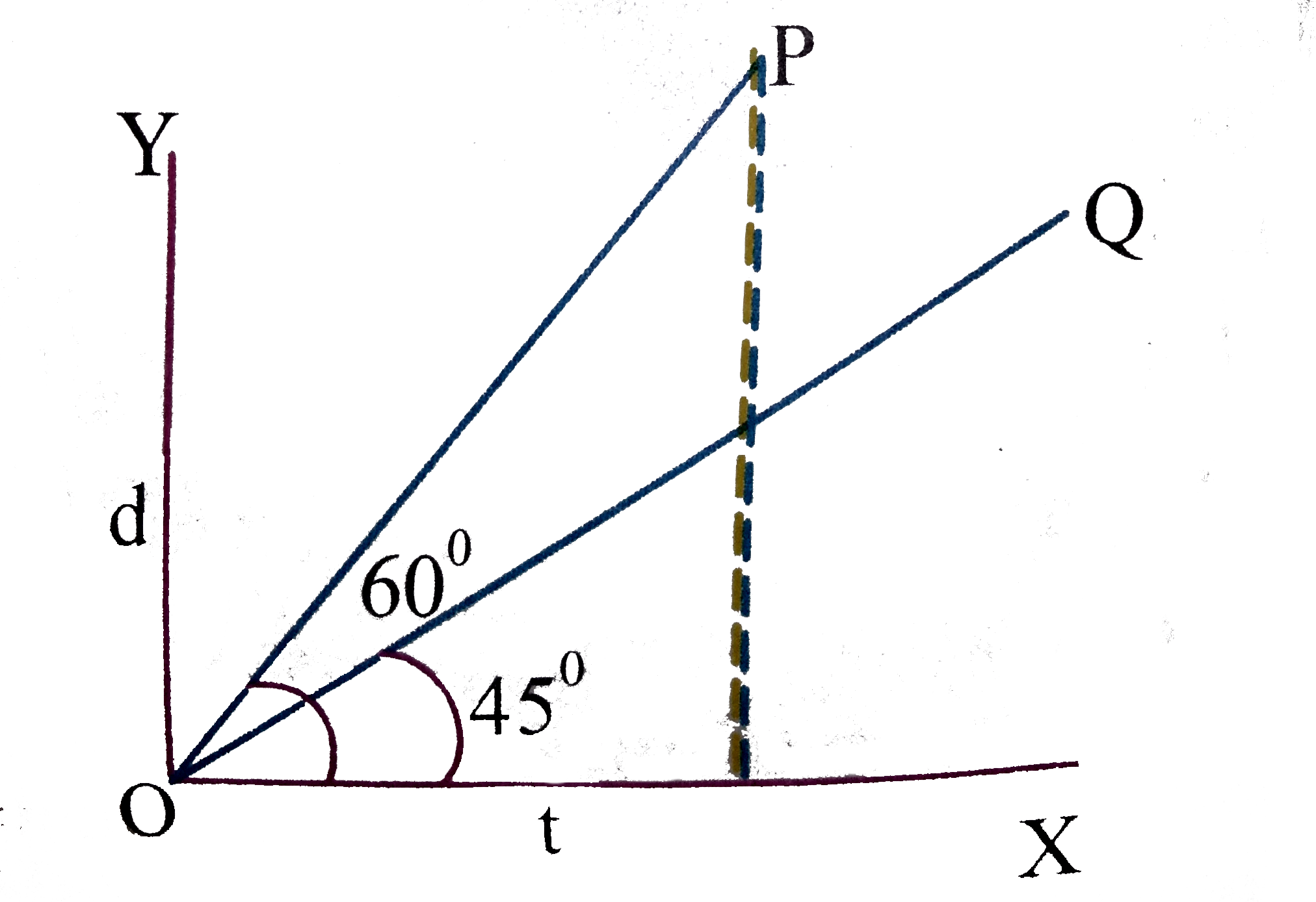
The displacement-time graphs of two bodies A and B are OP and OQ respectively. If ∠POX is 60∘ and ∠QOX is 45∘ the ratio of the velocity of A to that of B is
View Solution

