AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10 cm, CD=24 cm and the distance between AB and CD is 17 cm.Find the radius of the circle.
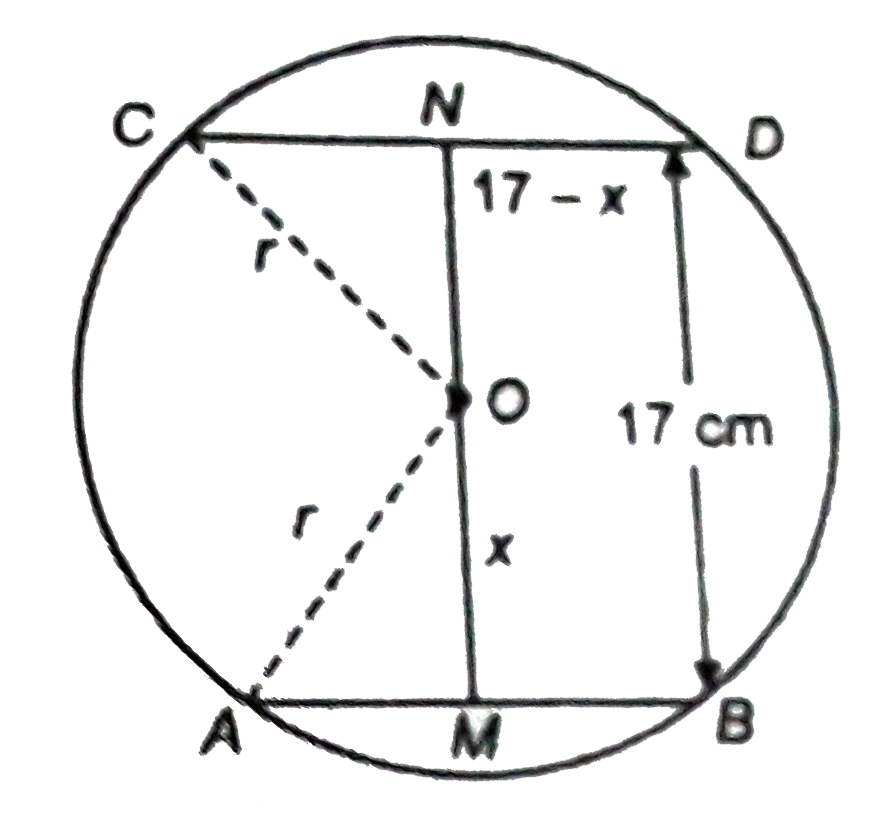
In the adjoining figure, O is the centre of the circle.
Here, AB=10cm
CD=24cm
OM and ON are perpendicular from centre O to AB and CD respectively.
∵AB∣∣CD
∴ MON is a transversal
Now, AM=12AB=12×10=5cm
CN=12CD=12×24=12cm
Let OM=x
∴ON=17−x
In ΔOMA,
OA2=OM2+AM2 (where OA=r is the radius of circle)
⇒r2=x2+52 ........(1)
∴ In ΔOCN,
OC2=ON2+CN2
⇒e2=(17−x)2+122 .........(2)
From eqs. (1) and (2).
x2+52=(17−x)2+12
⇒x2+25=289+x2−34x+144
⇒34x=289+144−25
=408
⇒x=40834=12
Put x=12 in eq. (1)
r2=x2+52
=122+52
=144+25
=169
⇒r=√169=13cm
∴ Radius of circle =13cm.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In a circle 10 cm long chord is at a distance of 12 cm form the centre. Find the length of a chord at a distance of 5cm from the centre.
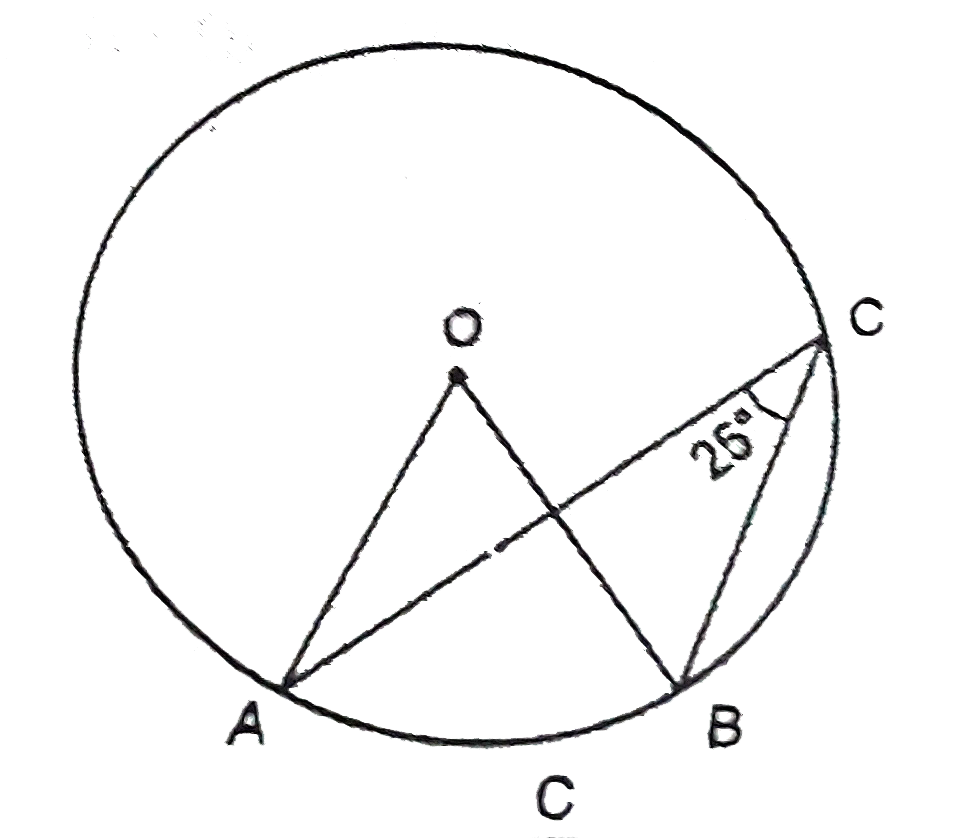
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
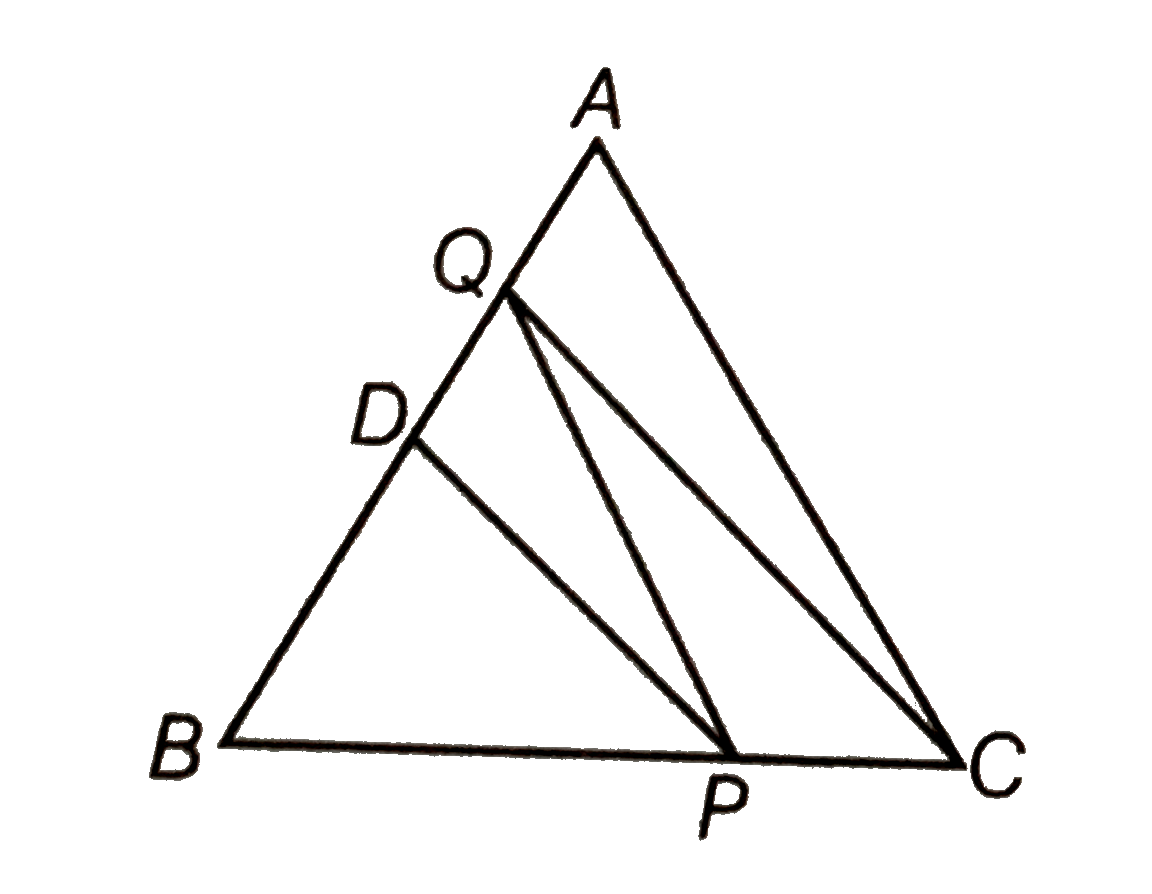
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
View SolutionPlot the following points on the same graph paper :
(i) (7,6)
(ii)(6,7)
(iii) (−4,3)
(iv) (3,−4)
(v) (−4,−4)
(vi) (−6,−4)
(vii)(7,−6)
(viii) (6,−7)
View SolutionAB तथा CD एक वृत्त की दो समांतर जीवाए हे जो केंद्र के विपरीत दिशाए में हे और दोनों के बीच की दूरी 17 cm हे, AB तथा CD की लम्बाई क्रमश, 10 cm तथा 24 cm तो वृत्त की त्रिज्या ज्ञात करे
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB =10cm , CD =24 cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionAB और CD एक वृत्त की दो जीवाएं है जहँ AB = 10 सेमी, CD = 24 सेमी और AB∣∣CD है। AB और CD के बीच की दूरी 17 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionAB और CD एक वृत्त की दो समान्तर जीवायें केन्द्र के दोनों ओर इस प्रकार हैं कि AB = 10 सेमी, CD = 24 सेमी ओर AB तथा CD के मध्य दुरी 17 सेमी है | वृत्त की त्रिज्या ज्ञात कीजिए |
View SolutionThe two parallel chords AB and CD with length of 10 cm and 24 cm in a circle situated on the opposite side of the centre. If the distance between two chards AB and CD is 17 cm , the calculate the length of the radiuys of the circle
View SolutionAB व CD एक वृत्त कि दो समांतर जिवाएँ इस प्रकार है कि AB=10 सेमी तथा CD=24 सेमी। यदि ये जिवाएँ केंद्र के विपरीत दिशाओं में है तथा उनकी बीच कि दूरी 17 सेमी है तो वृत्त कि त्रिज्या ज्ञात कीजिए।
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View SolutionIn the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View SolutionAB and CD are two chords such that AB = 10 cm , CD = 24 cm and AB // CD The distance between the chords is 17 cm . Find the radius of the circle.
View Solution
