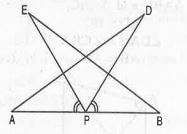
AB is a line segment and P is its midpoint. D and E are points on the same side of AB such that ∠BAD=∠ABE and ∠EPA=∠DPB. Show that AD=BE.
 Solution in Punjabi
Solution in Punjabi
Step by step video solution for AB is a line segment and P is its midpoint. D and E are points on the same side of AB such that angleBAD = angleABE and angleEPA = angleDPB. Show that AD=BE. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - SWAN PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 7.2
10 Videos
- TRIANGLES BOOK - SWAN PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 7.3
10 Videos
- SURFACE AREAS AND VOLUMES BOOK - SWAN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Objective Type Questions (Fill in the Blanks )
7 Videos
Similar Questions
In an isosclees triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O show that : OB=OC.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
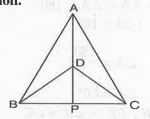 ).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
View SolutionTotal surface area of a cone = ..............
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
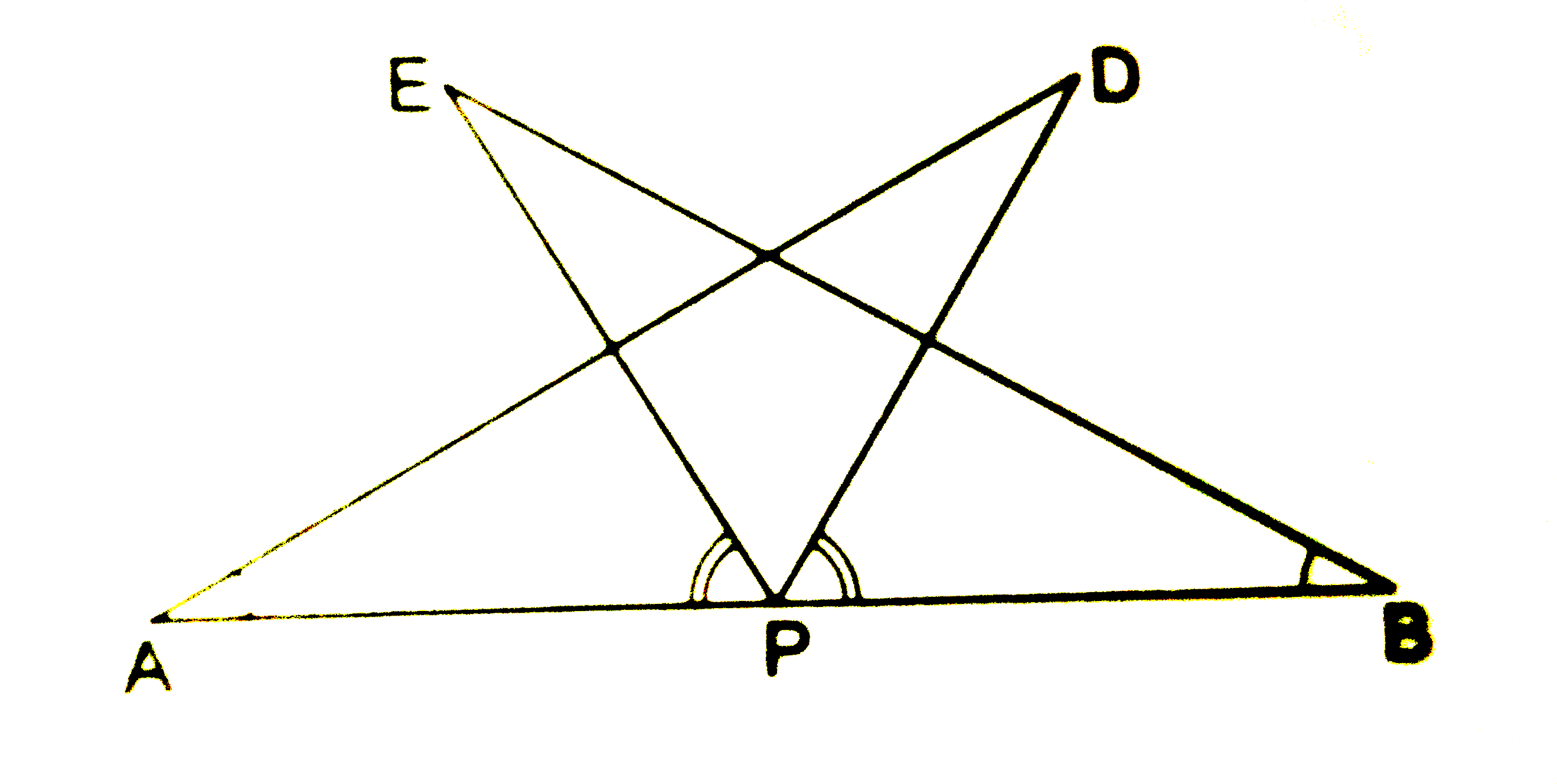
View SolutionAB एक रेखाखंड है और P इसका मध्य बिंदु है | D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD=∠ABE और ∠EPA=∠DPB है | (देखिए चित्र) | दर्शाइए कि
(i) ΔDAP≅ΔEBP
(ii) AD = BE
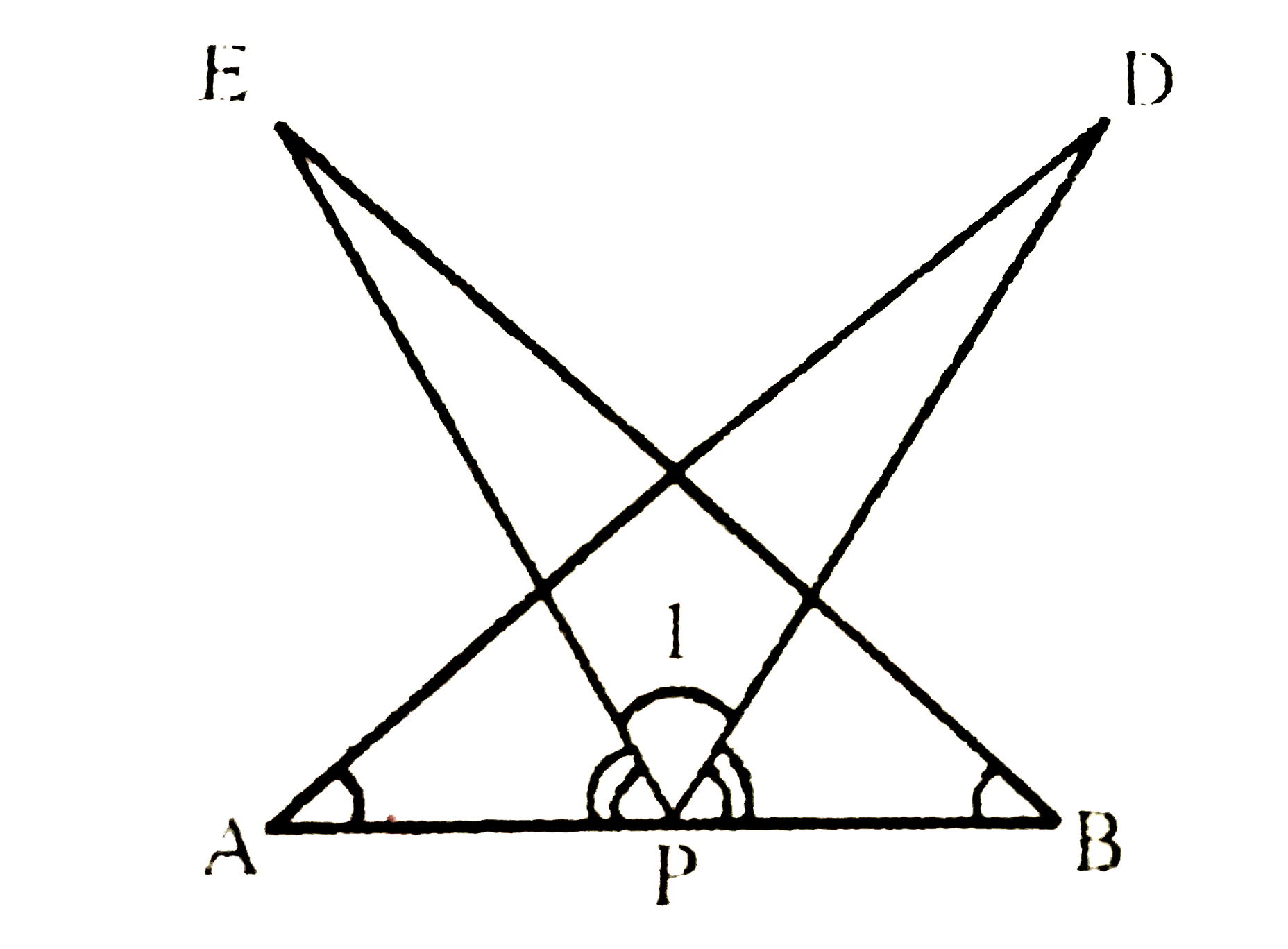
View SolutionAB एक रेखाखण्ड है तथा P इसका मध्यबिंदु है और AB की समान भुजा पर बिंदु D व E इस प्रकार है कि ∠BAD=∠ABE तथा ∠EPA=∠DPB तो सिद्ध कीजिए कि : ΔDAP≅ΔEBP
View SolutionLet AB be a line and P be its midpoint. To become angleBAD = angleABE And angleEPA = angleDPB Thus the points D and E are on the same side of AB (see Figure). (i) triangleDAP cong triangleEBP (ii) Show that AD = BE.
View SolutionAB एक रेखाखण्ड है और P इसका लम्ब-बिन्दु है | D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार है कि ∠BAD -= ∠ABE और ∠EPA -= ∠DPB है | ( देखिए आकृति ) दर्शाइए कि-
(i) ΔDAP ~-= ΔEBP
(ii) AD -= BE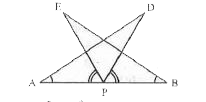
View Solution
