AB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P, prove that
ΔAPX≅ΔBPY
To prove that triangle ΔAPX is congruent to triangle ΔBPY, we will follow these steps:
Step 1: Identify the Given Information
We are given:
- Line segment AB
- Line segments AX and BY are equal and drawn on opposite sides of line AB
- AX∥BY
- AB and XY intersect at point P
Step 2: Analyze the Angles
Since AX∥BY, we can identify several pairs of angles that are equal due to the properties of parallel lines and transversals:
- Vertically Opposite Angles:
- ∠APX=∠BPY (because they are vertically opposite angles)
- Alternate Interior Angles:
- ∠AXY=∠BYP (since AX∥BY)
- ∠XAP=∠YBP (since AX∥BY)
Step 3: Establish Angle Congruences
From the above analysis, we have:
1. ∠APX=∠BPY (Vertically Opposite Angles)
2. ∠AXY=∠BYP (Alternate Interior Angles)
3. ∠XAP=∠YBP (Alternate Interior Angles)
Step 4: Use the Angle-Angle (AA) Criterion for Congruence
Since we have established that:
- ∠APX=∠BPY
- ∠AXY=∠BYP
- ∠XAP=∠YBP
We can conclude that the two triangles ΔAPX and ΔBPY are similar by the Angle-Angle (AA) criterion.
Step 5: Conclude the Proof
Since AX=BY (given that they are equal line segments), and we have established that the angles are equal, we can apply the criteria for congruence:
- ΔAPX≅ΔBPY by the Angle-Angle-Side (AAS) criterion.
Thus, we have proved that ΔAPX is congruent to ΔBPY.
We are given:
- Line segment AB
- Line segments AX and BY are equal and drawn on opposite sides of line AB
- AX∥BY
- AB and XY intersect at point P
Since AX∥BY, we can identify several pairs of angles that are equal due to the properties of parallel lines and transversals:
- Vertically Opposite Angles:
- ∠APX=∠BPY (because they are vertically opposite angles)
- Alternate Interior Angles:
- ∠AXY=∠BYP (since AX∥BY)
- ∠XAP=∠YBP (since AX∥BY)
From the above analysis, we have:
1. ∠APX=∠BPY (Vertically Opposite Angles)
2. ∠AXY=∠BYP (Alternate Interior Angles)
3. ∠XAP=∠YBP (Alternate Interior Angles)
Since we have established that:
- ∠APX=∠BPY
- ∠AXY=∠BYP
- ∠XAP=∠YBP
Since AX=BY (given that they are equal line segments), and we have established that the angles are equal, we can apply the criteria for congruence:
- ΔAPX≅ΔBPY by the Angle-Angle-Side (AAS) criterion.
Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Subjective Problems) ( Long Answer Type)
Explore 5 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Subjective Problems) ( Integer/Numerical Value Type)
Explore 5 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Subjective Problems) (Very Short Answer Type)
Explore 9 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
AB is a line segment. AX and BY are two equal line segments drawn on opposite sides of line AB such that AX∣∣BY. If AB and XY intersect each other at P,prove that APX≅BPY (ii) AB and XY bisect each other.
In the given figure, segment AXandBY are equa
View SolutionAB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AXBY. If AB and XY intersect each other P, prove that APX≅BPY AB and XY bisect each other.
View SolutionDraw a line segment equal to the sum of two line segments given in Fig.
View SolutionDivide line segment AB=10 cm into six equal parts.
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBP
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
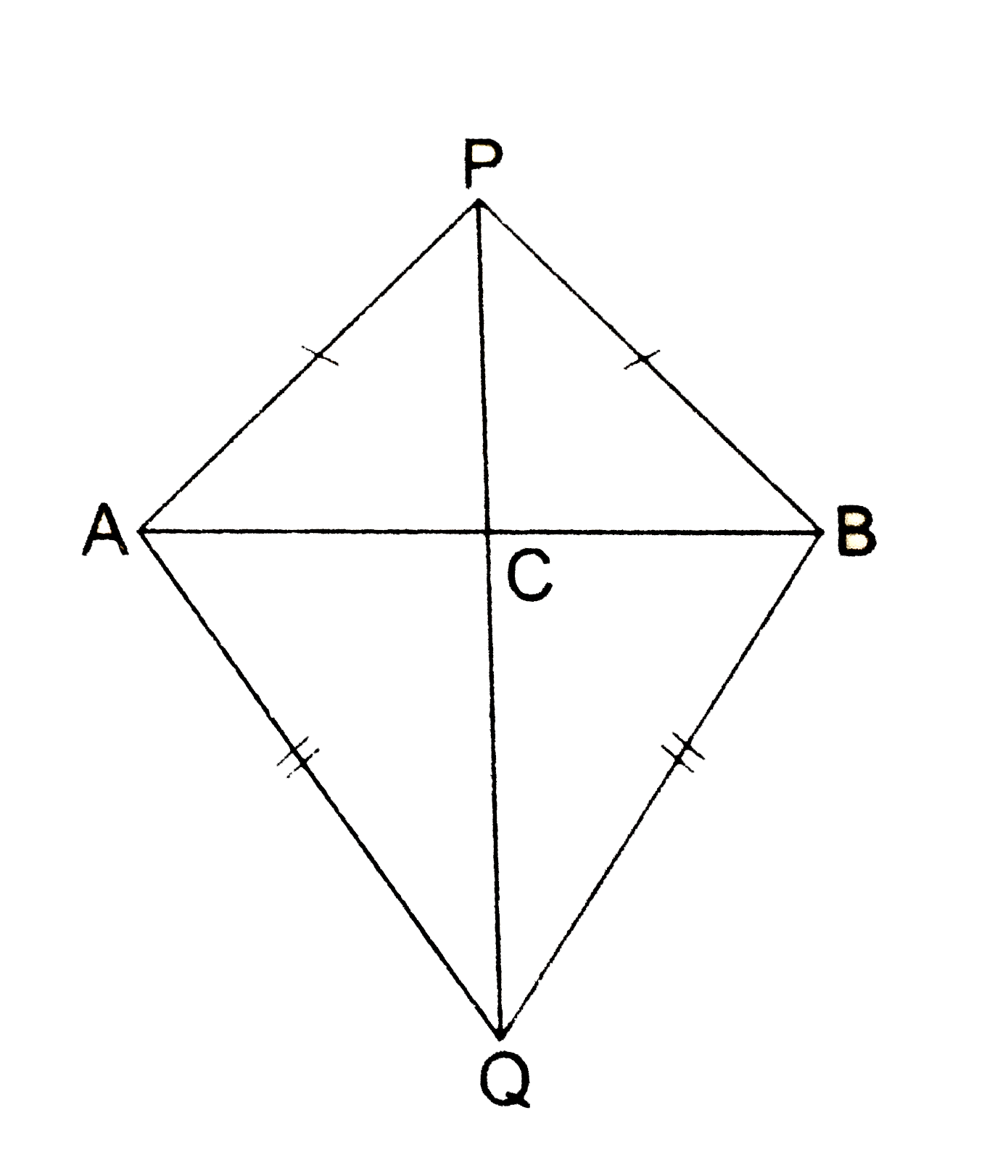
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
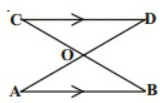
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
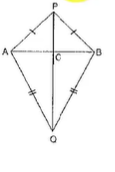
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View Solution