ABC is a right angled triangle in which ∠B=90∘andAB=BC. Find ∠Aand∠C.
To solve the problem, we need to find the angles A and C in triangle ABC, where angle B is 90 degrees and sides AB and BC are equal.
1. Identify the Given Information:
We know that triangle ABC is a right-angled triangle with angle B = 90 degrees, and sides AB = BC.
2. Use the Property of Isosceles Triangles:
Since AB = BC, triangle ABC is also an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, we can say:
∠A=∠C
3. Apply the Triangle Sum Property:
The sum of the angles in any triangle is 180 degrees. Therefore, we can write:
∠A+∠B+∠C=180∘
Substituting the known value of angle B:
∠A+90∘+∠C=180∘
4. Substitute Angle A with Angle C:
Since we established that ∠A=∠C, we can replace ∠C with ∠A:
∠A+90∘+∠A=180∘
This simplifies to:
2∠A+90∘=180∘
5. Solve for Angle A:
Subtract 90 degrees from both sides:
2∠A=180∘−90∘
2∠A=90∘
Now, divide both sides by 2:
∠A=90∘2=45∘
6. Find Angle C:
Since ∠A=∠C, we have:
∠C=45∘
Final Answer:
Thus, the angles are:
∠A=45∘and∠C=45∘
We know that triangle ABC is a right-angled triangle with angle B = 90 degrees, and sides AB = BC.
Since AB = BC, triangle ABC is also an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, we can say:
∠A=∠C
The sum of the angles in any triangle is 180 degrees. Therefore, we can write:
∠A+∠B+∠C=180∘
Substituting the known value of angle B:
∠A+90∘+∠C=180∘
Since we established that ∠A=∠C, we can replace ∠C with ∠A:
∠A+90∘+∠A=180∘
This simplifies to:
2∠A+90∘=180∘
Subtract 90 degrees from both sides:
2∠A=180∘−90∘
2∠A=90∘
Now, divide both sides by 2:
∠A=90∘2=45∘
Since ∠A=∠C, we have:
∠C=45∘
Thus, the angles are:
∠A=45∘and∠C=45∘
Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.3)
10 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.4)
6 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.1)
14 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
ΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that

ΔABD≅ΔACD
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionIn quadrilateral ABCD, AC=AD and AB bisects ∠A (see figure). Show that ΔABC≅ΔABD. What can you say about BC and BD ?
View SolutionThe weight (in kg) of 50 students are given below
40 45 55 62 50 51 56 69 61 36
60 56 69 38 35 63 57 50 57 48
40 63 53 64 47 42 56 51 42 60
55 39 64 57 64 44 66 35 59 59
73 62 49 63 37 63 54 72 44 60
Find the mean, median and mode respectively for the given data.
View SolutionIn a triangle ABC, if ∠A=70∘andAB=AC, then find the measures of ∠Band∠C.
View SolutionIn a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn a triangle ABC, if ∠A=∠B+∠C, the prove that triangle ABC is a right triangle.
View SolutionIn a triangle ABC, ∠A<∠B,∠B>∠C and ∠A=2∠C, prove that AC>BC>AB.
View SolutionABC एक समकोणत्रि त्रिभुज है, जिसमे ∠=90∘ और AB=AC है ∠B और ∠C कीजिएः
View Solutionयदि समकोण त्रिभुज ABC में ∠C=90∘,∠A=45∘ तथा BC=7 इकाई हो , तो ∠B,AB तथा AC का मान ज्ञात करो ।
View Solutionत्रिभुज ABC में ∠B समकोण है । यदि ∠A=∠C हो , तो sinAcosC+cosAsinC के मान ज्ञात करो ।
View Solutionत्रिभुज ABC में ∠B समकोण है । यदि ∠A=∠C हो , तो sinAsinB+cosAcosB के मान ज्ञात करो ।
View SolutionABC एक समकोण त्रिभुज है, जिसमे ∠A=90∘ और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
View SolutionABC is a right triangle in which ∠A=90∘ and AB = AC. Find ∠B and ∠C.
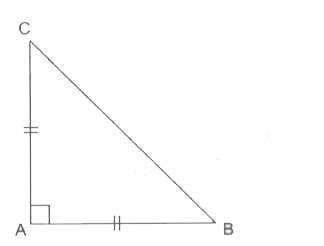
View SolutionABC is a right triangle. angleA = 90^@ And AB = AC. But angleB And angleC Find out.
View SolutionABC एक समकोण त्रिभुज है, जिसमे ∠A = 90∘ और AB = AC है | ∠B और ∠C ज्ञात कीजिए |

View Solution
