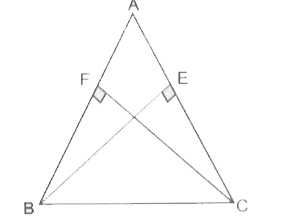
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
The correct Answer is:BE
Step by step video solution for ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.3
5 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
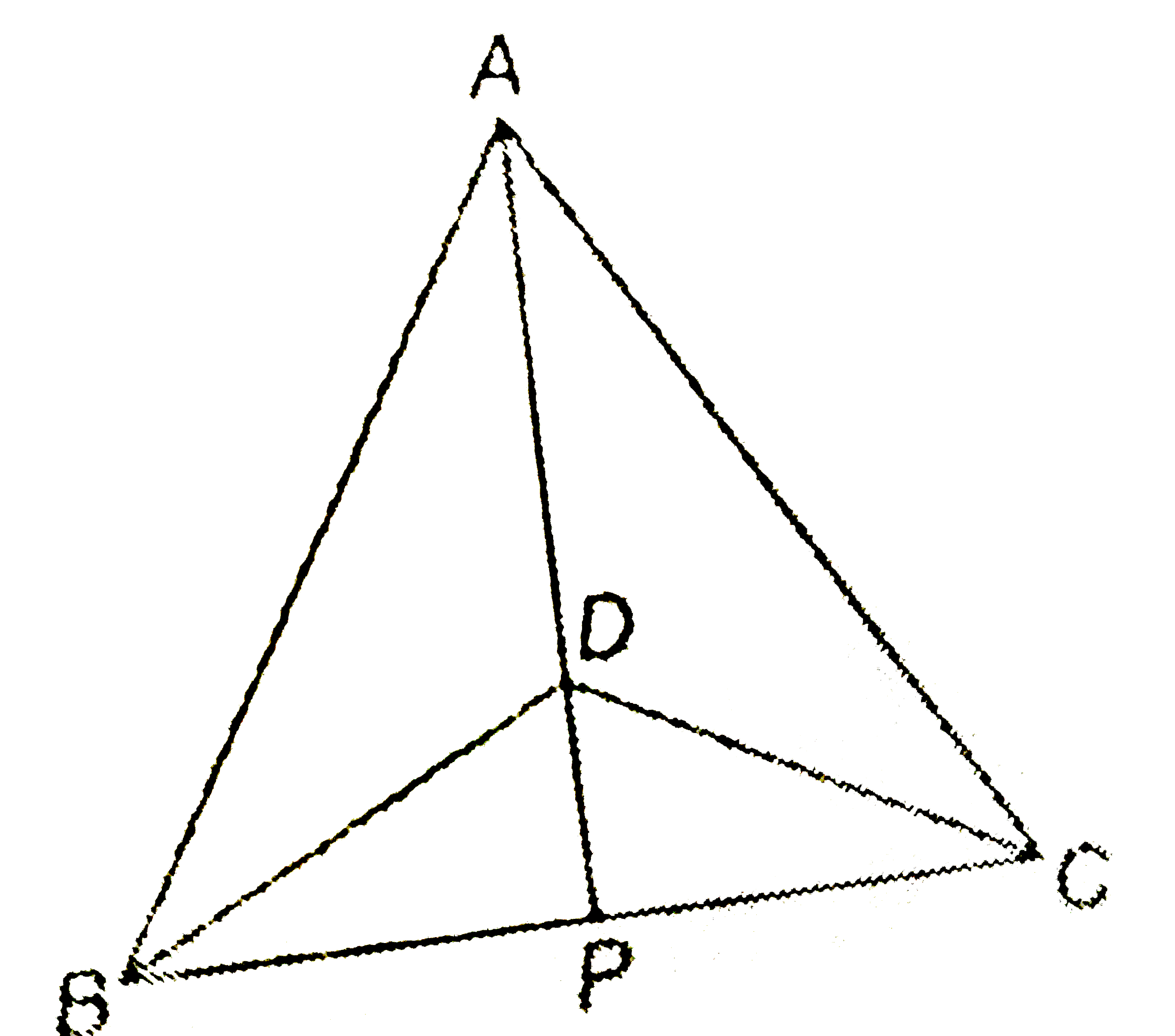
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
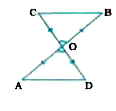
View SolutionIn the given figure, OA = OB and OD = OC. Show that
(i) ΔAOD≅ΔBOC and (ii) AD∣∣BC
View SolutionThe total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm2.
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
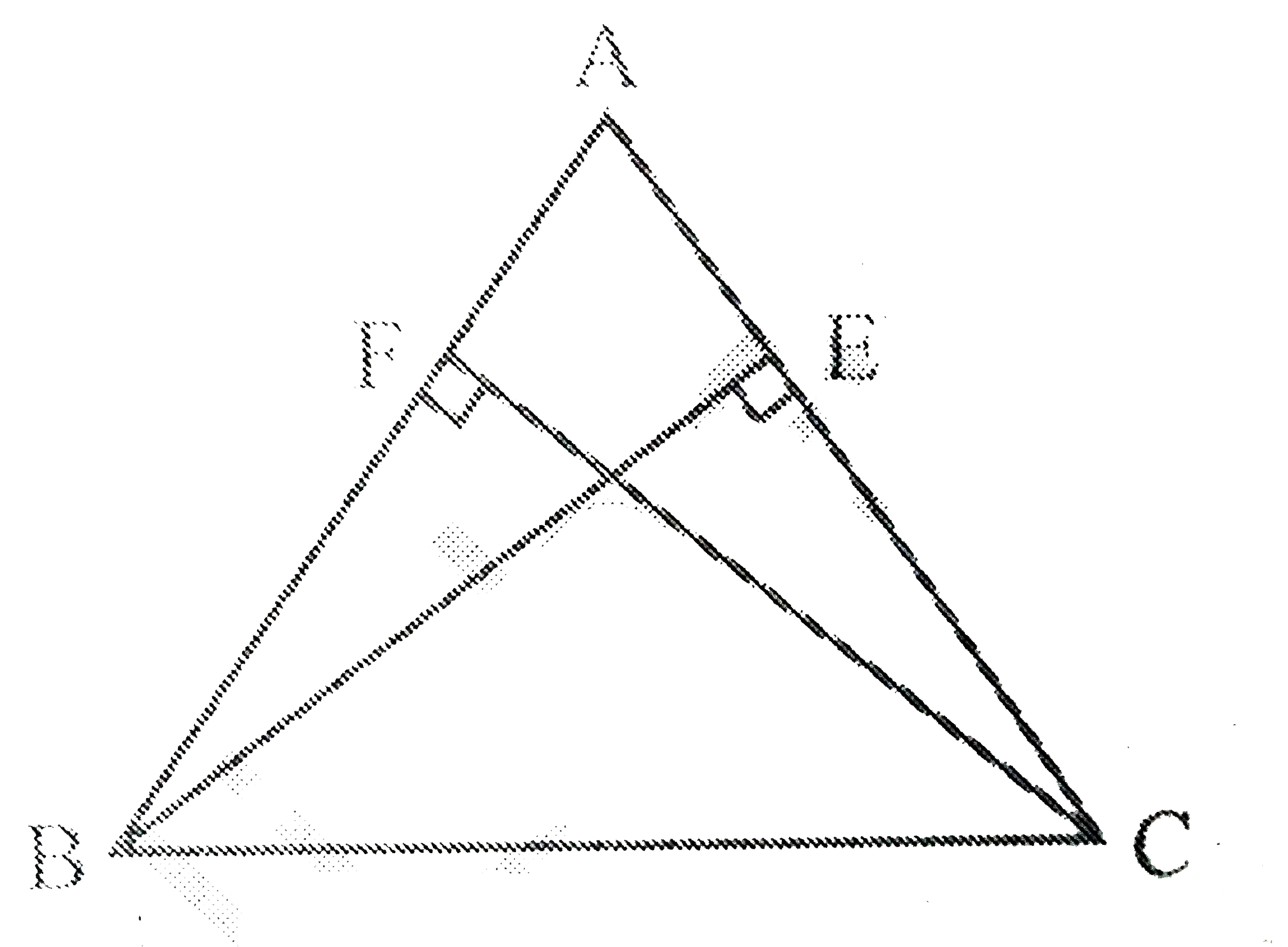
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलम्ब BE और CF खींचे गए हैं। दर्शाइए कि ये शीर्षलम्ब बराबर हैं।

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
View SolutionΔABC ఒక సమద్విబహు త్రిభుజము. సమాన భుజాలు AC,AB లకు గీసిన లంబాలు వరుసగా BE మరియు CF అయిన ఈ లంబాలు సమానమని చూపండి.
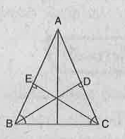
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
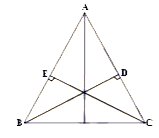
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
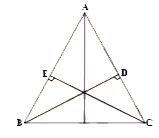
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
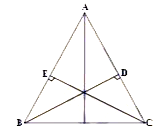
View SolutionABC एक समद्धिबाहू त्रिभुज है, जिसमे बराबर भुजाओ AC और AB पर क्रमश: शीर्षलम्ब BE और कफ खिचे गए है | ( देखिए आक्रति ) दर्शाइए कि ये शीर्षलम्ब बराबर है |

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
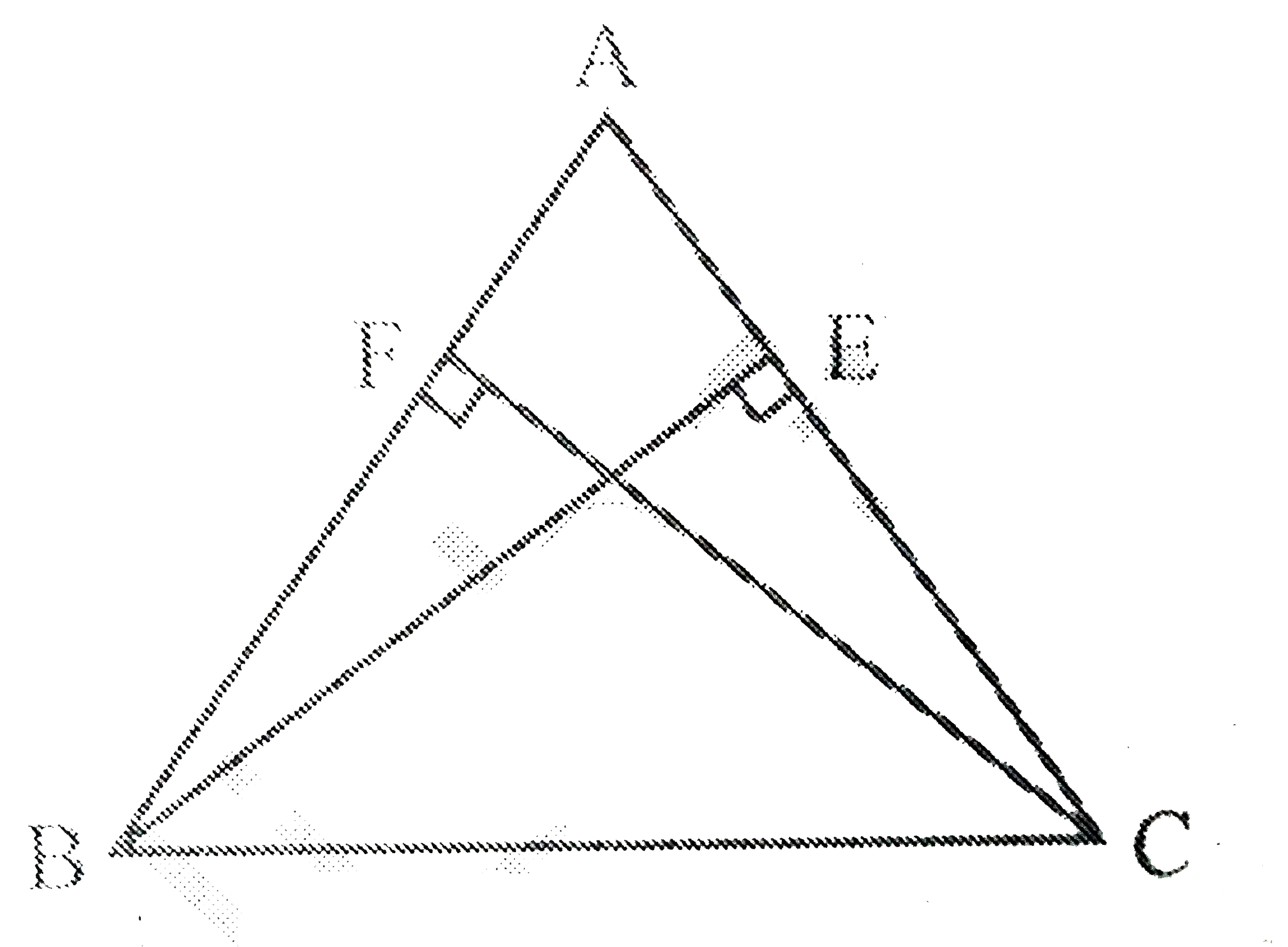
View Solution
