ABCD is a convex quadrilateral and 3, 4, 5, and 6 points are marked on the sides AB, BC, CD, and DA, respectively. The number of triangles with vertices on different sides is a. 270 b. 220 c. 282 d. 342
220
270
282
342
= Number of triangales with vertices on sides PQ, QR, and RS
+ Number of triangles with vertices on sides QR, RS and PS
+ Number of triangles with vertices on sides RS, PS and PQ
+ Number of triangles with vertices on sides PS, PQ and QR
=3C1×4C1×5C1×4C1×5C1×6C1+5C1×6C1×3C1+6C1×3C1×4C1
=60+120+90+72+=342.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Exercise
136 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
Statement-1: The number of zeros at the end of 100! Is, 24.
Statement-2: The exponent of prine p in n!, is
[np]+[np2]+.......+[npr]
Where r is a natural number such that Pr≤n<Pr+1.
View SolutionThe value of n∑r=1nPrr! is
View Solution7 women and 7 men are to sit round a circulartable such that there is a man on either side ofevery women. The number of seating arrangements is
View SolutionIf y=2x+k is a tangent to the curve x2=4y, then k is equal to
View SolutionTwo friends AandB have equal number of daughters. There are three cinema tickets which are to be distributed among the daughters of AandB . The probability that all the tickets go to the daughters of A is 1/20. Find the number of daughters each of them have.
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View SolutionABCD is a convex quadrilateral and 3, 4, 5, and 6 points are marked on the sides AB, BC, CD, and DA, respectively. The number of triangles with vertices on different sides is (A) 270 (B) 220 (C) 282 (D) 342
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solutionएक वृत्त, एक चतुर्भुज ABCD की चारों भुजाओं को अन्तः स्पर्श करता है। सिद्ध कीजिए कि-
AB + CD = AD + BC.
(अथवा) आकृति, में एक चतुर्भुज ABCD, O केन्द्र वाले वृत्त के परिगत इस प्रकार बनाई गई है कि भुजाएँ AB, BC, CD, तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R तथा S पर स्पर्श करती हैं। सिद्ध कीजिए कि
AB + CD = BC + DA
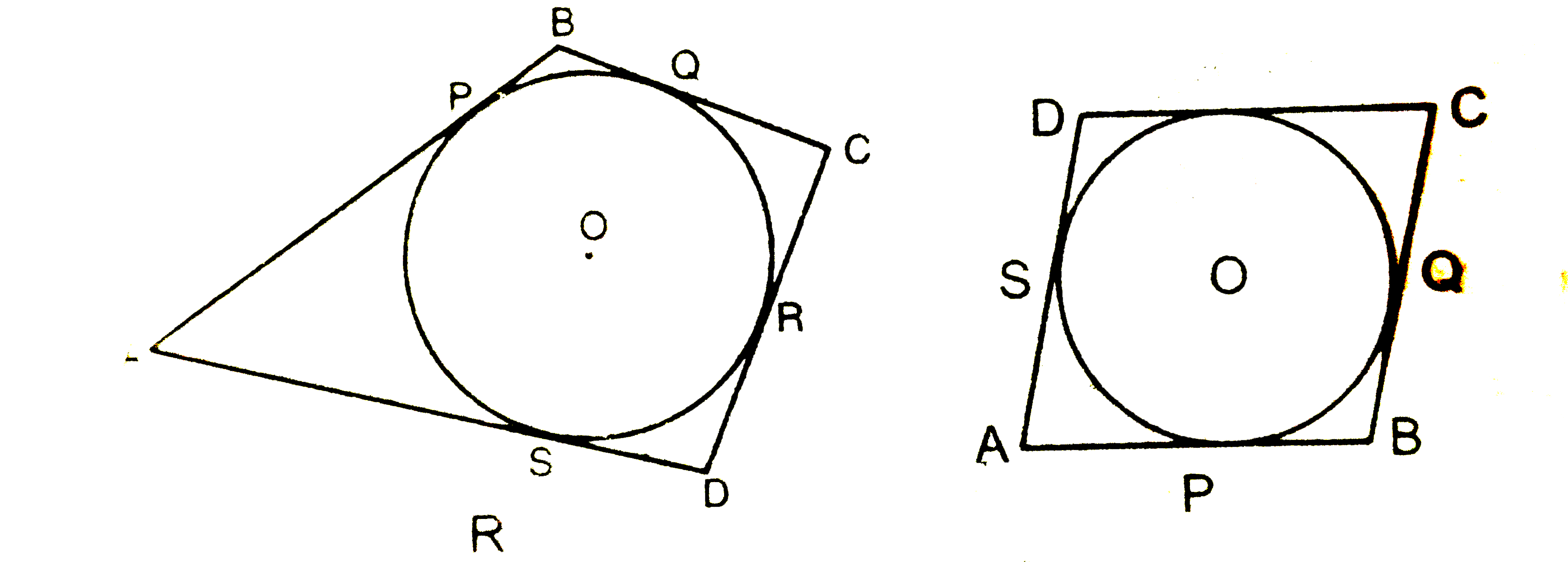
View Solutionवृत्त C(O,r) एक चतुर्भुज ABCD कि भुजाओं AB,BC,CD और DA को क्रमशः बिंदुओं P,Q,R और पर स्पर्श करता है। सिद्ध करो कि चतुर्भुज कि सम्मुख भुजाओं द्वारा केंद्र पर आन्तरिक कोणों का योग दो समकोण होता है।
View SolutionIf ABCD is a cyclic quadrilateral with AB = 6 , BC = 4, CD = 5, DA= 3 and ∠ABC=θ, then cos θ =
View SolutionABCD চতুর্ভুজের AB, BC, CD এবং DA বাহুগুলির ওপর 3, 4, 5 এবং 6 টি বিন্দু আছে। ওই বিন্দুগুলিকে শীর্ষবিন্দু ধরে গঠিত ত্রিভুজের সংখ্যা নির্ণয় করো।
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionABCD is a convex quadrilateral and 3, 4, 5, and 6 points are marked on the sides AB, BC, CD, and DA, respectively. The number of triangles with vertices on different sides is (A) 270 (B) 220 (C) 282 (D) 342
View SolutionConsider a rectangle ABCD having 5, 7, 6, 9 points in the interior of the line segments AB, CD, BC, DA respectively. Let α be the number of triangles having these points from different sides as vertices and β be the number of quadrilaterals having these points from different sides as vertices. Then (β−α) is equal to :
View Solution

