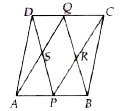
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram.(ii) DPBQ is a parallelogram.(iii) PSQR is a parallelogram
ABCD is a parallelogram
PQ=CQ=1/2DC
AP=PB=1/2AB
∴AP=CQ=1/2AB
AB||CD
∴AB||CQ
SQ||PR(AQCP)
PS||QR(DPBQ)
Similar Questions
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
(i) APCQ is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View Solution
Knowledge Check
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

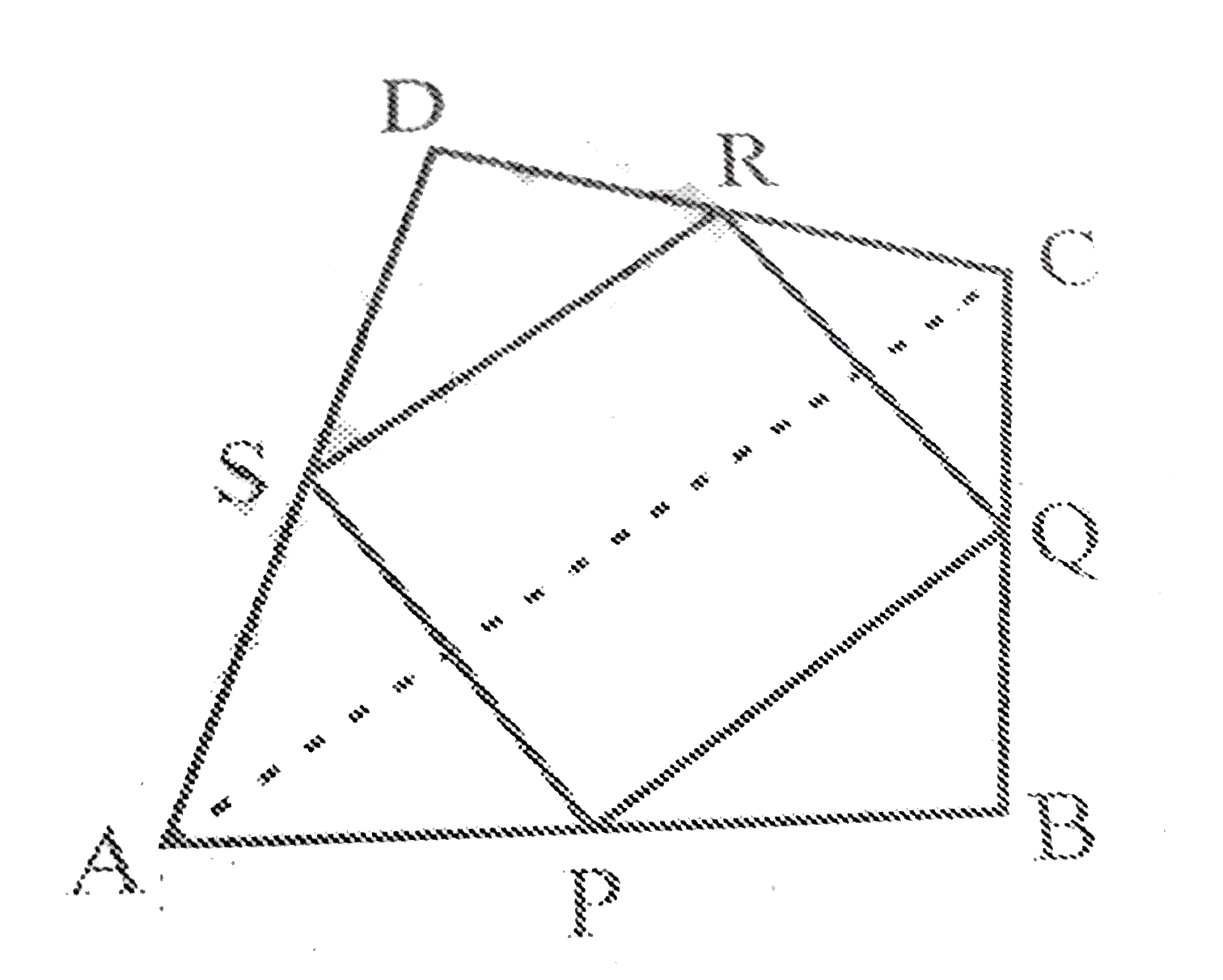
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
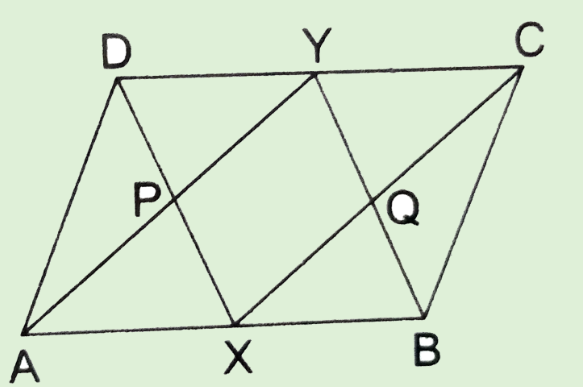
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
View Solution
